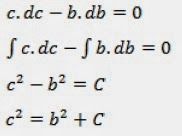Aktuaris: Lulusan Matematika dengan Masa Depan Cerah

Matematika merupakan salah satu ilmu murni yang dari tahun ke tahun menunjukkan peminat dengan angka relatif lebih kecil dibanding ilmu terapan. Terdapat anggapan bahwa sarjana matematika hanya bisa bekerja sebagai guru dan atau lowongan pekerjaan terbatas lainnya. Mitos tentang penilaian yang kurang tepat tersebut, justru bisa menghasilkan gaji besar dan  pilihan peluang pekerjaan yang lebih banyak. Tidak hanya menjadi guru, tetapi lulusan matematika ternyata bisa dibutuhkan dalam berbagai bidang, salah satu contohnya adalah Aktuaris.

Aktuaris adalah seorang ahli yang dapat mengaplikasikan ilmu keuangan dan teori statistik untuk menyelesaikan persoalan-persoalan bisnis aktual. Persoalan ini umumnya menyangkut analisis kejadian masa depan yang berdampak pada segi finansial, khususnya yang berhubungan dengan besar pembayaran pada masa depan dan kapan pembayaran dilakukan pada waktu yang tidak pasti. Para profesional yang memenuhi syarat dalam bidang aktuaria ini harus melalui pendidikan, pengalaman, dan sertifikasi. Secara umum, aktuaris bekerja dibidang konsultasi, perusahaan asuransi jiwa, pensiun dan investasi. Aktuaris juga sedang merambah di bidang-bidang lainnya, dimana kemampuan analitis diperlukan.

Aktuaria sering dikaitkan dengan Investasi dan Valuasi asset (Investment and Valuation), Risk management, asuransi dan dana pensiun, Karena tugas seorang aktuaris memang menghitung secara rinci segala resiko yang berkenaan dengan investasi dan resiko keuangan yang mungkin muncul karena kegiatan ekonomi. Pekerjaan seorang aktuaris tidak akan jauh dari urusan prediksi kalkulasi dan perumusan angka keuntungan dan kerugian atas segala kemungkinan yang akan terjadi pada masa depan, karena itulah tugas utamanya disebut Managing Uncertainty. Aktuaris meramal dan merumuskan masalah keuangan dengan pendekatan matematis dan statistika dan dapat dipertanggungjawabkan dengan rasio dan angka.

Gelar aktuaris di Indonesia atau Fellow Society of Actuaries of Indonesia (FSAI) diberikan oleh Persatuan Aktuaris Indonesia (PAI) setelah seorang individu menempuh 10 mata ujian yang diujikan. Pada umumnya aktuaris di Indonesia memiliki latar belakang pendidikan dari FMIPA Matematika maupun Statistika. Walaupun, ada sedikit yang berasal dari jurusan lain. Aktuaris di Indonesia banyak bekerja di perusahaan asuransi jiwa, sedangkan sisanya bekerja di dana pensiun, konsultan aktuaria, dan saat ini merambah ke dunia investasi.

Lulusan Jurusan Matematika tersebut membuka peluang untuk dapat bergabung dengan perusahaan besar kelas internasional dan berpotensi menjadi pakar analisa.  Sarjana lulusan ini akan sangat dicari petusahaan asuransi untuk menghitung prospek seorang klien asuransi dan berapa besar premi yang perusahaan asuransi bisa keluarkan untuk masing-masing klien. Aktuaris juga diyakini mampu untuk menunjang masa depan karena bisa menuai penghasilan besar bagi lulusannya. Kemampuan yang dibutuhkan seorang aktuaris di antaranya adalah kalkulus, matematika, statistika, teori probabilitas, ekonomi, keuangan, dan akutansi, ditambah kemampuan komunikasi.

Karir Aktuaris menduduki salah satu dari 10 profesi termahal di Amerika. Mengutip dariForbes,  tahun ini profesi aktuaris merupakan jenis pekerjaan terbaik nomor satu di Amerika Serikat (AS), disusul oleh profesi pembuat perangkat lunak dan analis sistem komputer. Pendapatan aktuaris di negara adidaya tersebut berkisar 85.229 USD. Tentu saja, ini adalah peluang yang besar untuk menghadapi masa depan yang cerah.

CarrerCast, sebuah situs karir, memperhitungkan 5 kriteria, yaitu dalam hal tuntutan fisik, lingkungan kerja, gaji, stres, dan kemungkinan mendapatkan pekerjaan, untuk melansir daftar prospek profesi terbaik hingga terburuk di tahun 2013. Hasil riset yang dilakukan mendapati profesi aktuaris adalah karir terbaik di tahun 2013, diikuti dengan insinyur biomedis, pembuat piranti lunak, audiolog, dan perencana keuangan. Dalam menyusun daftar tersebut, para peneliti menyusun data dari badan statistik tenaga kerja di AS, studi-studi asosiasi perdagangan, dan sebagainya. Data  ini jelas mendukung pernyataan bahwa profesi aktuaris sangat menjanjikan. Aktuaris, yang pekerjaannya berkaitan dengan menghitung kemungkinan risiko, umumnya di bidang asuransi, merupakan karir terbaik, karena menjadi profesi dengan gaji yang menggiurkan, dipadani dengan jadwal pekerjaan yang fleksibel.

Namun, Aktuaris di Indonesia belumlah begitu banyak walau diperlukan di banyak sektor seperti perbankan, perusahaan investasi atau penanaman modal, asuransi, badan-badan keuangan, konsultan keuangan, perumus kontrak, perencana keuangan, dll. Langkanya keberadaan aktuaris di Indonesia menjadi peluang besar bagi mahasiswa Matematika maupun Statistika untuk memperoleh pekerjaan sebagai aktuaris. Kekurangan aktuaris ini juga akan menjadi sebuah peluang besar untuk sarjana lulusan Matematika dalam berkarir. Dan, para siswa yang menyukai dan mampu dalam bidang matematika dan statistik, harus memperhitungkan profesi aktuaris yang makin langka di tengah-tengah profesi lain yang mulai jenuh, tentu saja dengan gaji yang menjanjikan.

Biografi John Napier: Penemu Logaritma dari Skotlandia

John Napier (1550 - 1617) lahir dekat Edinburgh, Skotlandia, pada tahun 1550. Ia adalah anak dari seorang tanah yang kaya yang meninggal pada saat ia masih muda. Ia belajar bahasa Latin, Yunani, dan matematika dari seorang guru privat. Pada usia 13 tahun, ia belajar di Universitas St. Andrews. Secara mengejutkan, ia tidak menyelesaikan gelar universitasnya akan tetapi pergi ke Eropa. Ia kembali ke rumah pada usia 21 tahun dan menikah setahun kemudian. Istri pertamanya meninggal dunia di tahun 1579, dan ia menikah lagi beberapa tahun kemudian.

Pada masa tersebut terjadi pergolakan untuk menentukan siapa penguasa kerajaan Inggris selanjutnya. Beberapa pertikaian muncul mengenai penentuan apakah Inggris akan menjadi negara Katolik atau Protestan. John Napier terlibat dalam tiga peristiwa untuk mendukung gereja Protestan sebagai pembelaannya terhadap King James VI dari Skotlandia.

Tidak mengherankan jika John terlibat dalam perang. Akan tetapi, ia akhirnya mengalihkan ketertarikannya pada bidang matematika dan astronomi. Ia ingin mencari cara untuk mengurangi waktu yang diperlukan pada saat menghitung bilangan yang panjang, seperti 57162958 x 6173298.

Pada tahun 1614, ia telah menyelesaikan buku pertamanya mengenai logaritma. Ia menemukan metode perkalian bilangan dengan menambah logaritmanya kemudian menggunakan invers logaritma untuk mendapatkan hasil akhir. Napier juga menemukan sehimpunan bilangan batang, yang sekarang disebut dengan Napier's bones, yang digunakan untuk mengalikan bilangan-bilangan. Penemuan-penemuan Napier adalah awal dari digunakannya penggaris geser dan kalkulator.

Napier meninggal dunia di Puri Merchiston pada tanggal 4 April 1617 dalam usia 67 tahun.

*Dari berbagai sumber

Logaritma

Jika n adalah logaritma dari a dengan bilangan pokok p, maka berlaku :

plog a = n <—> pn = a

Dengan catatan : a>0, p>0, dan p≠1

Setelah itu, barulah kita mempelajari sifat-sifat logaritma yang bisa kita terapkan di berbagai persoalan.

Sifat-sifat logaritma :
1. plog ( ab ) = plog a + plog b
2. alog an = n
3. plog (a/b) = plog a – plog b
4. plog 1 = 0
5. plog an = n . alog a
6. plog a . alog q = plog q
7. pnlog am = m/n plog a
8. plog p = 1
9. Pplog a = a

1. Bila bilangan pokok suatu logaritma tidak diberikan, maka maksudnya logaritma tersebut berbilangan pokok = 10.
   [log 7 maksudnya 10log 7 ]
2. lognx adalah cara penulisan untuk (logx)nBedakan dengan log xn = n log x

Logaritma

ac = b → ª log b = c
a = basis
b = bilangan yang dilogaritma
c = hasil logaritma
Sifat-sifat Logaritma
ª log a = 1
ª log 1 = 0
ª log aⁿ = n
ª log bⁿ = n • ª log b
ª log b • c = ª log b + ª log c
ª log b/c = ª log b – ª log c
ªˆⁿ log b m = m/n • ª log b
ª log b = 1 ÷ b log a
ª log b • b log c • c log d = ª log d
ª log b = c log b ÷ c log a

Gottfried Wilhelm Leibniz (1646-1716)

a. Biografi

Leibniz di lahirkan di Leibzig, Jerman. Ayahnya adalah seorang profesor Filasafat Moral, meninggal ketika Leibniz masih kecil. Sewaktu mahasiswa ia mempelajari ilmu hukum, filsafat, dan juga matematika. Pada usia 20 tahun dia sudah mendapat gelar Doktor. Leibniz adalah seorang ahli filsafat dari Jerman yang tidak hanya seorang ahli filsafat saja melainkan juga seoarang yang ahli dalam ilmu pengetahuan yang universal, sebab ia adalah seorang yang ahli hukum, ahli sastra, ahli ilmu pasti dan ilmu alam, serta ahli teologia dan ahli sejarah.

b. Metafisika

Sama seperti pendahulunya, Descartes dan Spinoza, maka Leibniz juga memfokuskan teori-teorinya kepada aspek metafisika, yakni permasalahan substansi. Kalau seorang Descartes menyebutkan bahwa di alam ini substansi mewakili tiga hal, yakni tuhan, jiwa dan materi, Spinoza (dengan hanya satu substansi: Allah atau alam). Demikian Leibniz mengatakan bahwa terdapat banyak substansi dan jumlahnya tidak terhingga.

Leibniz berpendapat bahwa alam raya ini atau segala sesuatu yang ada tidak berasal dari prinsip satu substansi saja melainkan berasal dari banyak substansi yang jumlahnya tidak tehingga. Dengan kata lain, yang membentuk daya hidup alam ini tidak berasal dari prinsip satu substansi saja, akan tetapi prinsipnya berasal dari eksistensi plural yang menjadikannya hidup. Seperti sebuah mobil yang terangkai dari macam-macam benda yakni busi, dinamo, ban, aki dan lain-lain, yang sebagaimana benda-benda penyusun mobil tersebut juga tersusun dari macam-macam benda lain, maka berkat adanya rangkaian benda-benda tersebut mobil dapat hidup dan beroperasi, jika masing-masing benda yang merangkai mobil itu dilepas satu-persatu, maka mobil tersebut dipastikan tidak berfungsi. Dengan demikian, Leibniz menjadi seorang yang pluralis.

Seperti itulah pandangan Leibniz tentang substansi yang jumlahnya tidak terbatas dan tak terhingga. Ia menyebut substansi-substansi itu dengan nama monad. (monos = satu, monad=satu unit). Monad merupakan substansi sederhana yang akan menyusun substansi yang lebih kompleks. Dikatakan substansi yang sederhana karena adanya penyusunan. Karena penyusunan itu tak lain dan tak bukan dari susunan substansi sederhana. Dengan kata lain bahwasanya substansi yang kompleks merupakan susunan substansi-substansi sederhana. Substansi yang sederhana ialah substansin yang terkecil yang tidak dapat dibagi lagi. Monade ini bukanlah atom, tetapi suatu titik yang bersifat murni metafisis, tanpa bentuk dan tanpa keluasan di dalam ruang.

Jika dalam matematika yang terkecil adalah titik, dan dalam fisika disebut dengan atom, maka dalam metafisika disebut dengan monade. Terkecil dalam pendapat leibniz bukan berarti sebuah ukuran, melainkan sebagai tidak berkeluasan dan tidak mempunyai bagian-bagian. Apa pun yang tidak mempunyai ukuran tuntulah tidak berbentuk, tidak dapat dibagi. Maka yang dimaksud dengan monade bukan sebuah benda. Monade-monade bukanlah sebuah kenyataan jasmaniah melainkan kenyataan mental, yang terdiri dari persepsi dan hasrat. Leibniz membayangkan monade sebagai “force primitives” (daya purba) yang tidak materiil, melainkan spiritual. Setiap Monade tak lain adalah un miroir vivant de l’univers cermin hidup alam semesta.

Setiap monad berbeda satu dengan yang lain. Allah juga monad, tetapi bukan sembarang monade, melainkan monade purba yang merupakan aktivitas murni, actus purus. Dan tuhan (sesuatu yang supermonad dan satu-satunya monad yang tidak dicipta), Pencipta monad-monade itu. Maka karya Leibniz tentang ini diberi judul Monadologi (study tentang monad) yang ditulisnya 1714.

Sebagai substansi nonmaterial, monade bersifat; 1. Abadi, tidak bisa dihasilkan, ataupun dimusnahkan; 2. Tidak bisa dibagi (bertentangan dengan “substansi” keluasan. Descartes yang mengandaikan sifat dapat dibagi); 3. Individual atau berdiri sendiri, sehingga tidak ada monade yang identik dengan monade lain (bertentangan dengan substansi Spinoza yakni bahwa substasi hanya tuhan atau Alam); 4. Mewujudkan kesatuan yang tertutup atau tidak berjendela, seolah-olah sesuatu bisa masuk atau keluar; Menurut sifatnya monade tidak mempunyai jendela-jendela, tempat suatu bisa masuk atau keluar. Jika demikian bagaimanakah monade-monade dapat mengenal realitas di luarnya? Pertanyaan ini dijawab oleh leibnizt bahwasanya tiap monade mencerminkan semua monade yang lain, sehingga dalam dirinya setiap monade mengenal realitas seluruhnya; 5. Mampu bekerja berkat daya aktif dari dalam dirinya sendiri. Kerja dari dan oleh dirinya sendiri ini terdiri dari kegiatan mengamati (perceptio) dan meninginkan (appetitions). Karena sifat-sifat inilah, Leibniz mendefinisikan monade sebagai atom-atom sejati dari alam dan hanya apabila monade tersebut ada dalam “jasad-jasad organic”, maka monade-monade itu akan menjadi “prinsip kehidupan”.

Usaha mengamati (perceptio) sebuah monade menurut Leibniz terdiri dari “merekam” atau seperti sebuah cermin memantulkan alam semesta sebagai keseluruhan. Keberadaan semua monade tersebut mempunyai tugas untuk bekerja sama membentuk suatu struktur dunia yang harmonis dan sesungguhnya monade-monade ini mencerminkan alam semesta, akan tetapi pencerminan tersebut bukan berasal dari alam itu sendiri yang memberikan, akan tetapi Tuhan-lah yang memberikannya sebuah sifat spontan yang menyebabkan refleksisme. Keberadaan semua monad tersebut mempunyai tugas untuk bekerja sama membentuk suatu struktur dunia yang harmonis.

Monade menurut Leibniz ada tiga macam berdasarkan tingkat kejelasan pengamatan. pertama, monade yang hanya memiliki gambaran gelap dan sama sekali tidak disadari, yakni monade-monade yang menyusun benda-benda anorganik. Kedua, monade yang telah memiliki gambaran agak terang yaitu, yaitu monade yang member pengenalan inderawi dan memori, misalnya monade-monade penyusun manusia dan hewan. Ketiga, monade yang memiliki gambaran yang terang dan kesadarn diri (apperceptio), yakni jiwa manusia yang mengenal hakikat segala sesuatu secara sadar dan mampu mengungkapkan apa yang dilihatnya ke dalam suatu definisi.

Selain mengamati tiap monade juga menginginkan (appetitions).. Menurut Leibnizt tiap monade memiliki daya dorong dari dalam dirinya sendiri untuk bergerak secara pogresif, mulai dari usaha untuk mendapat gagasan yang baru dan agak jelas(perceptio) hingga mendapat gagasan yang jelas dan di sadari (apperceptio).

c. Argumen Lebniz Tentang Bukti Adanya Tuhan

Dalam permikirannya, Leibniz bermaksud untuk membuktikan eksistensi wujud (Tuhan). Bagaimana keberadaan Tuhan itu benar-benar “ada” didalam kehidupan manusia. Ia membuktikan eksistensi Tuhan dengan konsepnya tentang monade-monade.

Leibniz berusaha membuktikan keberadaan Tuhan dengan empat Argumen. Pertama, ia mengatakan bahwa manusia memiliki ide kesempurnaan, maka adanya Tuhan terbukti. Bukti ini disebut dengan ontologism. Kedua, ia berpendapat adanya alam semesta dan tidak lengkapnya membuktikan adanya sesuatu yang melebihi alam semesta ini, dan yang transenden ini disebut dengan Tuhan. Ketiga, ia berpendapat bahwa kita selalu ingin mencapai kebenaran abadi dan bahwa kebenaran itu tak bisa di hasilkan manusia menunjukkan adanya adanya pikiran abadi yaitu “Tuhan”. Keempat, Leibniz mengatakan bahwa adanya keselarasan antara monade-monade membuktikan bahwa pada awal mula ada yang mencocokan mereka satu sama lain, yang mencocokkan itu adalah Tuhan.

d. Manusia

Manusia adalah kumpulan monade-monade, yang karena keselarasan yang ditentukan sebelumnya, telah di hubungkan oleh suatu “ikatan substansi” (vinculum substantiale). Menurut tubuhnya, manusia termasuk monade pertama, menurut nafsu dan perasannya termasuk monade kedua dan menurut jiwanya manusia termasuk monade ketiga. Seluruh organisme terdiri dari monade-monade yang hidup. Namun ada monade pusat satu, yang mengatur semuanya yang secara khusus tampil sebagai asas hidup, atau sebagai jiwa makhluk yang hidup. Kesatuan antara tubuh dan jiwa disebabkan karena adanya kerja sama antara keduanya dan beralaskan “ikatan substansi ” (vinculum substantiale), yang bersandar kepada keselarasan yang di tentukan sebelumnya (harmonia praestabilita). Hal ini di ibaratkan seperti dua alroji yang disusun oleh tukang alroji yang ahli sedemikian rupa sehingga keduanya berjalan dengan cara yang sama dan menunjukkan waktu yang sama tanpa ada pengaruh kausal di antaranya.

Dalam hubungan jiwa dengan tubuh, Leibniz berpendapat bahwa tubuh berhubungan erat dengan jiwa. Tidak seperti pandangan Descartes yang menganggap tubuh hanya merupakan teman tidur (bersifat pasif), Leibniz memandang bahwa tubuh tidak terus-terusan terdiri dari ukuran, bentuk, dan gerakan, melainkan kita harus mengenali sesuatu yang terdapat dalam tubuh yang menghubungkan dengan jiwa, Leibniz menyebutnya dengan subtansi—Leibniz menyebut subtansi dengan monad. Ia menyebutkan bahwa di dalam manusia terdapat sesuatu yang menyerupai jiwa, Leibniz menyebutnya dengan subtansi (monad), yang memberi daya kepada tubuh untuk melakukan aktivitas. Menurutnya alam merupakan kumpulan dari berbagai monad, ia menolak ide ketunggalan monad Spinoza.

e. Kesimpulan

Ada banyak substansi di dunia menurut Leibniz, substansi tersebut disebut juga dengan monade, berbeda dengan Spinoza yang mengatakan bahwa substasi hanya ada satu yaitu Tuhan atau alam, dan begitu pula dengan Descartes yang membagi subtansi menjadi tiga, yaitu ; Tuhan, Pemikiran, dan keluasan Tuhan telah menciptakan dunia sebelumnnya, sehingga dunia yang sedang berjalan sekarang adalah dunia yang telah ditentukan oleh Tuhan sebelumnya, ia mengibaratkan sebagai sebuah jam dinding.

25 Macam Pembuktian Teorema Pythagoras

        Siapa yang belum mendengar “Teorema Pythagoras”? sejak di sekolah dasar kita telah diperkenalkan dengan sifat yang terdapat pada segitiga siku-siku tersebut. Sebagai tambahan wawasan dan pengetahuan bagi para guru, berikut ini disajikan penjelasan singkat mengenai sejarah teorema Phytagoras serta 25 cara membuktikannya.

Teorema Pythagoras merupakan salah satu teorema yang telah dikenal manusia sejak peradaban kuno. Nama teorema ini diambil dari nama seorang matematikawan Yunani yang bernama Pythagoras. Pythagoras lahir di pulau Samos, Yunani, sekitar tahun 570 SM. Sesuai dengan nasehat gurunya Thales, Pythagoras muda mengunjungi Mesir sekitar tahun 547 SM dan tinggal di sana.

Bangsa Mesir kuno telah mengetahui bahwa segitiga dengan panjang sisi 3, 4 dan 5 akan membentuk sebuah sudut siku-siku. Mereka menggunakan tali yang diberi simpul pada beberapa tempat dan menggunakannya untuk membentuk sudut siku-siku pada bangunan-bangunan mereka termasuk piramid. Diyakini bahwa mereka hanya mengetahui tentang segitiga dengan sisi 3, 4 dan 5 yang membentuk segitiga siku-siku, sedangkan teorema yang berlaku secara umum untuk segitiga siku-siku belum mereka ketahui.

     Di Cina, Tschou-Gun yang hidup sekitar 1100 SM juga mengetahui teorema ini. Demikian juga di Babylonia, teorema ini telah dikenal pada masa lebih dari 1000 tahun sebelum Pythagoras. Sebuah keping tanah liat dari Babilonia pernah ditemukan dan memuat naskah yang kira-kira berbunyi sebagai berikut: “4 is length and 5 the diagonal. What is the breadth?”

Pythagoras-lah yang telah membuat generalisasi dan  membuat teorema ini menjadi populer. Secara singkat teorema Pythagoras berbunyi:

Pada sebuah segitiga siku-siku, kuadrat sisi miring (sisi di depan sudut sikusiku) sama dengan jumlah kuadrat sisi-sisi yang lain.

1.    Pembuktian dari Sekolah Pythagoras

Sifat pada segitiga siku-siku ini sebenarnya telah dikenal berabad-abad sebelum masa Pythagoras, seperti di Mesopotamia, juga Cina. Tetapi catatan tertulis pertama yang memberi bukti berasal dari Pythagoras. Bukti dari sekolah Pythagoras tersebut tersaji pada gambar di bawah.

Perhatikan bahwa:

 

Luas daerah hitam pada gambar (1) adalah a² + b²

Luas daerah hitam pada gambar (2) adalah c²

Dengan demikian a² + b² = c²

2.    Pembuktian lain menggunakan diagram Pythagoras

Bukti berikut ini lebih sederhana tetapi menggunakan sedikit manipulasi aljabar. Keempat segitiga siku-siku yang kongruen disusun membentuk gambar di bawah ini.

Dengan menghitung luas bangun bujur sangkar yang terjadi melalui dua cara akan diperoleh:

(a + b)                     =          c² + 4. ½ ab

a² + 2ab + b²          =          c² + 2 ab

a² + b²                     =          c²

3.    Bukti dari Astronom India Bhaskara (1114 - 1185)

Bukti berikut ini pertama kali terdapat pada karya Bhaskara (matematikawan India, sekitar abad X). Bangun ABCD di atas berupa bujursangkar dengan sisi c. Di dalamnya dibuat empat buah segitiga siku-siku dengan panjang sisi a dan b.

Dengan konstruksi bangun tersebut, maka:

Luas PQRS + 4  x luas ABQ    =      luas ABCD

(b – a)² + 4 x ½ . ab                 =      c²

b² – 2ab + a² + 2ab                   =      c²

a² + b²                                       =      c²

4.    Pembuktian Teorema Pythagoras oleh Presiden J. A. Garfield

Pembuktian ini berasal dari J. A. Garfield pada tahun 1876. Luas daerah trapesium di bawah ini dapat dihitung dengan dua cara sehingga teorema Pythagoras dapat dibuktikan sebagai berikut.

Luas trapesium       =          (alas + atas)/2. tinggi               =          (a + b)/2. (a + b)

Di lain pihak, luas trapesium          =          2. ½ ab + ½ c²

Sehingga, (a + b)/2. (a + b)            =          2. ½ ab + ½ c²

a² + 2ab + b²                                  =          2ab + c²

a² + b²                                             =          c²

5.    Bukti menggunakan Garis Tinggi dan Sifat Segitiga Sebangun (Pembuktian Baskhara yang Kedua)

Perhatikan gambar berikut:

Segitiga ABC sebangun dengan segitiga ACD sehingga b/c = c₁/c atau b² = c . c₁ ... (1)

Segitiga ABC sebangun dengan segitiga CBD sehingga a/c = c₂/a atau a² = c . c₂ ... (2)

Dari (1) dan (2) diperoleh:

a² + b² = c . c₁ + c . c₂

a² + b² = c (c₁ + c₂)

a² + b² = c . c

a² + b² = c²

6.    Bukti menggunakan Transformasi

Misal segitiga ABC siku-siku di C. Putarlah segitiga ABC sejauh 90⁰ berlawanan arah dengan putaran jarum jam dengan pusat rotasi C. Akan diperoleh segitiga A’B’C’ yang berimpit dengan segitiga ABC.

½ a²                        =          (1)

½ b²                                =          (2) + (3)

------------------------------------ +

½ a² + ½ b²             =          (1) + (2) + (3)

                               =          [(1) + (2)] + (3)

                               =          ½ cx + ½ cy

                               =          ½ c (x + y)

                               =          ½ c.c

                               =          ½ c²

Dengan mengalikan dua pada setiap ruas maka akan diperoleh a² + b² = c²

7.    Bukti dengan Dasar Perbandingan lagi

Diberikan segitiga ABC yang siku-siku di C. Kalikan setiap sisi dengan c. Lalu bentuk dua segitiga sebangun dengan ABC seperti pada gambar di atas. Dengan perbandingan sisi pada segitiga-segitiga sebangun akan diperoleh panjang sisi-sisi yang lain pada bangun di samping. Dari konstruksi tersebut jelas c² = a² + b².

Bukti sejenis ini terdapat pula dalambeberapa buku dan publikasi, seperti oleh Birkhoff.

8.    Bukti dengan “Bayangan”

Perhatikan bahwa kelima gambar di bawah ini memuat daerah gelap dengan luas yang sama (menggunakan konsep kesamaan luas bangun-bangun datar).

9.    Bukti dengan “Putaran”

Perhatikan proses dari diagram di atas.

Luas daerah gambar awal   =   a² + b² + 2. ½ . ab

Luas daerah gambar akhir  =    c² + 2. ½. Ab

Oleh karena transformasi di atas tidak mengubah ukuran, maka kedua daerah tersebut sama luasnya, sehingga dengan mengurangi masing-masing oleh ab atau mengambil kedua bangun segitiga siku-siku akan diperoleh:

a² + b² = c² (Sumardyono, 2003)

10.    Bukti dengan cara “Geser, Potong, lalu Putar”

Perhatikan bukti geometris berikut ini, dengan cara menggeser, memotong, dan memutar.

(Sumardyono, 2004)

11.    Bukti dari Euclid

Bukti berikut ini pertama kali diberikan oleh Euclid. Perhatikan gambar di bawah ini.

DBQE        =          NLBD ..... kedua bangun konruen

                   =          MLBC...... alas sama-sama BL dengan tinggi tetap BD

                   =          SRBC ...... alas sama-sama BC dengan tinggi tetap BR

                   =          a²

ADEP         =          KNDA..... kedua bangun konruen

                   =          KMCA ..... alas sama-sama AK dengan tinggi tetap AD

                   =          UTCA ...... alas sama-sama AC dengan tinggi tetap AU

                   =          b²

c²    = BDQE + ADEP

       =     a²     +    b²

12.    Bukti dari Leonardo da Vinci

Diberikan segitiga siku-siku ABC. Buatlah segitiga JHI kongruen dengan ABC. Maka segiempat ABHI, JHBC, ADGC, dan EDGF adalah kongruen.

Bukti teorema Pythagoras dilakukan sebagai berikut:

Luas ADGC + luas EDGF = luas ABHI + luas JHBC

                 Luas ADEFGC = luas ABCJHI

Kedua bangun memuat dua segitiga yang kongruen dengan segitiga ABC, sehingga:

Luas ADEFGC – 2. Luas ABC     =          luas ABCJHI – 2. Luas ABC

Luas ABED + luas BCGF             =          luas ACJI

13.    Bukti dengan cara “Tambah lalu Geser”

Susunlah empat segitiga siku-siku yang kongruen dengan segitiga ABC seperti pada gambar sebelah kiri, lalu tambahkan sebuh bujur sangkar dengan luas b – a.

Maka diperoleh:

Luas KMNPQR     =          luas KSQR + luas MNP

                               =          a² + b²

Kemudian pindahkan segitiga 1 dan 4 sehingga membentuk bangun di sebelah kanan. Bangun yang terbentuk adalah bujur sangakar dengan sisi c, sehingga luasnya c². (Sumardyono, 2003)

14.    Bukti dari Liu Hui (pada 3 Masehi)

Bukti berikut bersifat geometris. Tetapi Anda dengan mudah dapat membuktikannya secara aljabar.

15.    Bukti dari Tsabit ibn Qorra

Bukti berikut berasal dari Tsabit ibn Qorra (836-901) dan merupakan generalisasi Teorema Pythagoras. Diberikan sebarang segitiga ABC. Buatlah titik A’ dan B’ pada AB sedemikian sehingga < BA’C = < AB’C = < CAB’ (untuk gambar atas <CAB’ tumpul dan untuk gambar bawah < CAB’ lancip). Dengan demikian tampak bahwa segitiga ABC, segitiga CBA’ dan segitiga ACB’ saling sebangun.

Kesebangunan ini mengakibatkan:

AC/BA = A’B/CB (pandang segitiga CBA’ dan ABC )

AC/AB = AB’/AC (pandang segitiga ACB’ dan ABC)

Sehingga akan diperoleh BC² + AC² = AB(A’B + AB’)

Apabila sudut C siku-siku maka A’ = B’ dan Teorema Pythagoras terpenuhi.

                                          

16.    Bukti dari Pappus

Bukti berikut berasal dari Pappus (sekitar 300 M) dan merupakan suatu generalisasi. Buat sebarang segitiga ABC. Lalu buat sebarang jajargenjang CADE (di sisi CA) dan sebarang jajargenjang CBFG (di sisi BC). Kemudian panjang DE dan FG hingga bertemu, katakan di H. Kemudian lukis AL dan BM sejajar dan sama panjang dengan HC. Maka:

Luas CADE    =          luas CAUH     =          luas SLAR

Luas CBFG                 =          luas CBVH     =          luas SMBR

--------------------------------------------------------------------------- +

Luas CADE + luas CBFG                              =          luas ABML

Bila segitiga ABC adalah segitiga siku-siku (dengan sudut siku-siku di C) serta jajargenjang di sisi CA dan BC merupakan bujursangkar, maka akan diperoleh Teorema Pythagoras.

17.    Pembuktian dengan Segitiga Sama Sisi

Buat segitiga siku-siku dengan panjang sisi a, b, dan c.

Kemudian buat segitiga sama sisi dengan panjang a, b, dan c di setiap sisi-sisinyasehinggaakan tampak seperti gambar berikut.

Dari gambar di atas,diketahui bahwa luas segitiga sama sisi pada sisi miring sama dengan jumlah segitiga sama sisi lainnya.

Untuk segitiga dengan panjang sisi k, l, dan m maka luas segitiga tersebut adalah

18.    Pembuktian dengan Identitas Trigonometri Pythagoras

Buat segitiga siku-siku dengan panjang sisi a, b, dan, c seperti gambar berikut.

Kemudian dengan menggunakan trigonometri untuk menentukan sinus dan cosinus sudut Ө yaitu sebagai berikut.

Hubungan antara sinus dan cosinus dinamakan sebagai identitas trigonometri Pythagoras yang mendasar. Sehingga pada trigonometri kita ketahui bahwa

Hubungan antara sinus dan cosinus dinamakan sebagai identitas trigonometri Pythagoras yang mendasar. Sehingga pada trigonometri kita ketahui bahwa.

19.    Pembuktian denan Persamaan Differensial

Pertama gambar segitiga siku-siku ABC seperti gambar berikut

b diperpanjang ke titik D yaitu sisi db, c juga diperpanjang dengan sisi dc. Terdapat dua sisi segitiga yang sebangun yaitu segitiga AED (EA tegak lurus terhadap sisi miring) dan segitiga ABC seperti gambar berikut.

oleh karena itu rasio atau perbandingan sisi-sisi pada segitiga tersebut harus sama, yaitu:

Dapat ditulis sebagai berikut

Perhatikan gambar, apabila b = 0, maka a harus berhimpit terhadap c. Artiya a = c. Maka konstanta = c² = a² sehingga c² = b² + a² terbukti.

20.    Pembuktian Thabit Ibn Qurra

Buat persegi panjang dengan panjang a dan b, kemudian disusun berdampingan seperti gambar berikut.

Luas bangun di atas adalah persegi besar dan persegi kecil yaitu a² + b².

Persegi di atas kita gabungkan, kemudian buat garis sedemikian rupa sehingga akan tampak seperti gambar di bawah, dimana sisi c menjadi sisi miring.

Selanjutnya segitiga kita potong dan tempatkan di bagian lain yaitu samping kanan dan bagian atas sehingga akan tampak seperti gambar berikut.

Bangun yang terbentuk adalah sbuah bujur sangkar dengan luas c².

21.    Pembuktian John Kawamura

Pembuktian ini ditemukan oleh siswa SMA yang dilaporkan oleh Chris Davis, guru geometrinya di Head-Rouce School, Oakland, CA.

Kedua diagonal tegak lurus memiliki panjang c, sehingga daerah yang sama dengan c²/2 sehingga

c²/2 = Luas bangun ABCD

                    = Luas BCD + Luas ABD

        = a.a/2 + b.b/2

 c² = a² + b² terbukti

22.    Pembuktian Tao Tong

ABC dan BED dua buah segitiga yang kongruen. E pada AB.

Luas ABD = BD.AF/2 = DE.AB/2

Berdasarkan gambar di atas diperoleh

(c-x)/2 = b.b/2.x = CF  (diperoleh dari kesamaan BD dan AC pada segitiga BFC dan ABC).

x = a²/2

23.    Pembuktian dengan beberapa segitiga yang sebangun.

Berdasarkan gambar di atas diperoleh

y/b = b’/c, x/a = a’/c + cx = aa’ + bb’

maka cc’ = aa’ + bb’

24.    Pembuktian dengan dua trapesium yang kongruen

Pembuktianini ditemukan oleh seorang siswa SMA, Jamie deLemos.

Kuas dari trapesium tersebut adalah

(2a+2b)/2.(a+b)

Di lain pihak

2.a.b/2 + 2b.a/2 + 2.c²/2

Dari dua persamaan tersebut diperoleh:

a² + b² = c²

25.    Pembuktian dari weininjieda dari Cina

Misal CE = BC = a, CD =AC =b, F titik potong DE dan AB.

Segitiga CED kongruen dengan segitiga ABC, misal DE = AB = c.

AC tegak lurus dengan BD

BE tegak lurus dengan AD, dan 

ED tegak lurus dengan AB. Maka diperoleh

Luas segitiga ABD = Luas segitiga ABE + Luas segitiga ACD + luas segitiga BCE

Akan diperoleh persmaan

c(c+EF) = EF. C + b² + a²

yang bentuk sederhananya

c² = b² + a²