A Review of Hydraulic Fracturing Simulation

Abstract

Along with horizontal drilling techniques, multi-stage hydraulic fracturing has improved shale gas production significantly in past decades. In order to understand the mechanism of hydraulic fracturing and improve treatment designs, it is critical to conduct modelling to predict stimulated fractures. In this paper, related physical processes in hydraulic fracturing are firstly discussed and their effects on hydraulic fracturing processes are analysed. Then historical and state of the art numerical models for hydraulic fracturing are reviewed, to highlight the pros and cons of different numerical methods. Next, commercially available software for hydraulic fracturing design are discussed and key features are summarised. Finally, we draw conclusions from the previous discussions in relation to physics, method and applications and provide recommendations for further research.

1 Introduction

As a technique to fracture underground rock formation using pressurized fluid, hydraulic fracturing has been applied extensively in such diverse areas as reservoir stimulation, in-situ stress estimation, caving and fault reaction in mining, and environmental subsurface remediation [3, 141, 221, 270, 375]. In the context of reservoir stimulation, shale gas production has been significantly improved by the wide adoption of multi-stage hydraulic fracturing and horizontal drilling techniques. Hydraulic fracturing plays a critical role in recovering oil and gas from unconventional reservoirs, where it creates fracture networks to provide the transport path in tight formations. Since the first field test performed on a gas well at the Hugoton field in 1947 [44], hydraulic fracturing has been extensively researched by both academia and industries using experimental tests, field trials and numerical simulations [83, 168].

From the viewpoint of geomechanics, the hydraulic fracturing process involves three stages: fracture initiation, fracture propagation, and flow-back. The resulting fracture network is determined by the specific hydraulic fracturing treatment (e.g. perforation strategy, property of proppant and fracturing fluid, and injection schedule) and the local geological conditions (e.g. rock properties, distribution of natural fractures). The complexity of predicting the induced fracture network is manifold: (1) the fluid flow inside fractures is inherently coupled with the rock deformation and fracture propagation; (2) a range of multiscale and multi-physics processes are involved, such as the interaction between natural and hydraulic fractures, leakoff, proppant transport, and rock heterogeneity [154, 367]; and (3) geological and operational conditions are difficult to model accurately due to the lack of data and high cost associated. To make the study of hydraulic fracturing more tractable, some aspects of the problem need to be simplified or even ignored in analytical and numerical investigations, which has led to the development of many different modelling approaches with varying applicability and limitation.

Hydraulic fracturing modelling has been extensively studied by researchers in both petroleum engineering and fracture mechanics [18, 139, 189]. Numerous hydraulic fracturing models have been developed to improve the hydraulic fracturing treatment design or to understand some specific mechanisms such as screen-out, near wellbore tortuosity, etc. The period between the 1950s and the 1980s saw the development of a series of classic hydraulic fracturing models, such as the Kristianovich-Geertsma-de Klerk (KGD) model, the Perkins-Kern-Nordgren (PKN) model, the pseudo 3D (P3D) model, and the planar 3D (PL3D) model. Until recently, the P3D and PL3D models remain popular in commercial simulators for hydraulic fracturing design. During the recent decades, a wider range of numerical methods have been applied and adapted to model hydraulic fracturing, such as the finite element method (FEM), the extended finite element method (XFEM), and the discrete element method (DEM).

In this review article, we aim to provide a state-of-the-art and comprehensive overview of hydraulic fracturing modelling techniques. Specifically, the review will focus on three aspects: (1) the underlying physical processes involved in hydraulic fracturing; (2) the classical and modern hydraulic fracturing models; and (3) commercial simulators for hydraulic fracturing design and evaluation. The remaining paper is organized as follows. In Sect. 2 we analyse the various physical processes relevant to hydraulic fracturing and their corresponding mathematical descriptions. Then, the historical development of hydraulic fracturing models and the more modern methods are explained in Sects. 3 and 4, respectively. Next, Sect. 5 provides a brief overview on commercial simulators used by the oil and gas industry for hydraulic fracturing modelling. Finally, concluding remarks are made in Sect. 6, highlighting both the research achievements to date and the outstanding technical challenges.

Fig. 1

Hydraulic fracturing as a multiscale and multi-physics process

2 Physical Processes and Mathematical Models

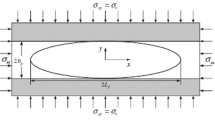
Simply speaking, hydraulic fracturing is a process to fracture underground rocks by injecting pressurized fluid into the formation, for which a schematic illustration is given in Fig. 1. With respect to the underlying physics, hydraulic fracturing involves three basic processes: (1) deformation of rocks around the fracture; (2) fluid flow in the fracture; and (3) fracture initiation and propagation [3, 179, 313]. These basic processes are briefly reviewed in this section together with their corresponding mathematical models. In addition to these basic physical processes, hydraulic fracturing also involves a number of other physical phenomena that are often considered as secondary processes in various analytical and numerical models. These secondary physical processes are also reviewed in this section, to provide a full picture of hydraulic fracturing as a multiscale and multi-physics process.

2.1 Three Basic Processes

2.1.1 Rock Deformation

The deformation of rocks is determined by rock properties and related boundary conditions such as fluid pressure and in-situ stresses. As the rock formation is heterogeneous in nature, it is difficult to exactly represent realistic rock properties in a numerical model. In addition, rock deformation often exhibits elastoplastic behaviour that is further complicated by its porosity. Due to these intrinsic complexity, it is necessary to introduce some assumptions to make the coupled problem more manageable. One of the most widely adopted simplification is linear elasticity expressed as:

$$\begin{aligned} \varvec{\sigma } =\varvec{C}:\varvec{\varepsilon }\ \end{aligned}$$

(1)

where $\varvec{\sigma }$ denotes the Cauchy stress tensor, $\varvec{\varepsilon }$ the linear strain tensor, and $\varvec{C}$ the elastic tensor determined by Poisson’s ratio $\nu$ and Young’s modulus E. The equilibrium condition of rocks is expressed as

$$\begin{aligned} \nabla \varvec{\sigma } +\rho \varvec{g}=\rho \ddot{\varvec{u}} \end{aligned}$$

(2)

where $\rho$ denotes the local density of rock, $\varvec{g}$ the gravity acceleration, and $\varvec{u}$ the displacement.

In some cases such as a straight fracture in 2D space or a planar fracture in 3D space, the fracture width could be computed directly according to some analytical solutions derived from the elasticity theory [50, 116, 177]. These equations are commonly used in such classic hydraulic fracturing models as PKN, KGD, radial model, P3D and PL3D.

Poroelasticity has been widely adopted to consider the effect of porosity and pore pressure in rock formations [29, 239]. Based on Biot’s consolidation theory [26], additional parameters are introduced to describe the properties of rocks, including Biot modulus, effective stress coefficient, rock permeability, and existing pore pressure etc. (see Sect. 2.4 for more details). Other constitutive models, such as hyper elasticity and elasto-brittle relations, have also been used to describe the deformation of rock formations [188, 191], and more details are discussed in Sect. 4.

The rock deformation is computed and presented in different ways, depending on the specific numerical discretization approach adopted (see Sect. 4). In continuum-based methods, such as the boundary element method (BEM) and FEM, the rock deformation is computed based on a discretization mesh and is presented by nodal values. In discontinuum-based methods, the rock deformation is computed and presented by the movement of particles or blocks. The strategy to compute rock deformation also affects the other numerical elements in a hydraulic fracturing model, and it represents a critical feature of hydraulic fracturing simulators.

2.1.2 Fluid Flow in the Fracture

Hydraulic fracturing differs from the traditional fragmentation problems because of the intrinsic coupling between fracture propagation and fluid flow, and as a result it is arguably more challenging to model. One of the simplest ways to consider the effect of fluid flow within the numerical framework of hydraulic fracturing is to apply a uniform fluid pressure on the fracture surface [134]. However, this overly simplified approach can cause significant modelling error, with the exception of certain special cases with low-viscosity fluid and high-toughness formation. A more rational approach to modelling fluid flow in fractures is based on the lubrication theory, which recognizes the fact that the aperture of a hydraulic fractures is always much smaller than its height and length [85, 378, 394, 395]. The application of lubrication theory in hydraulic fracturing modelling is extremely popular, and the Poiseuille’s law (or cubic law) is widely used to relate the flow rate with the pressure gradient along the hydraulic fracture. For the fluid flow in a two-dimensional hydraulic fracture, the Poiseuille’s law is expressed as:

$$\begin{aligned} q=-\frac{{{w}^{3}}}{12\mu }\frac{dp}{ds} \end{aligned}$$

(3)

where q is the flow rate, w is the fracture width, $\mu$ is the viscosity of the fracturing fluid, p is the fluid pressure, and s is the local coordinate aligned with the tangential direction to the fracture path.

Taking into account the leakoff effect, the continuity equation is expressed as:

$$\begin{aligned} \frac{dw}{dt}+\frac{dq}{ds}+{{q}_{L}}=0 \end{aligned}$$

(4)

where ${{q}_{L}}$ is the leakoff flow rate.

The Poiseuille’s law and the continuity equation listed above are widely used in 2D discrete fracture analysis and can be easily extended to the 3D discrete fracture analysis by considering the flow rate and pressure gradient in different directions [239, 282]. In smeared fracture models, the Poiseuille’s law is often implemented with a fracture permeability [52, 180, 329]

$$\begin{aligned} {{k}_{f}}=\frac{{{w}^{2}}}{12} \end{aligned}$$

(5)

where the fracture width w is a virtual value computed according to the element deformation in smeared fracture models.

The lubrication theory captures the pressure drop along the hydraulic fracture, and it is easy to implement and computationally cheap. As a result, it has been the most widely used fluid model in hydraulic fracturing simulation. Poiseuille’s law is only valid for laminar flow, which is the main flow regime during hydraulic fracturing operations. However, turbulent flow may also occur as the injection flow rate and properties of fracturing fluid vary over a large range in hydraulic fracturing [179, 393].

2.1.3 Fracture Propagation

As an essential part of hydraulic fracture models, fracture criterion is used to determine the fracture propagation. In hydraulic fracturing simulations, the choice of fracture criterion largely depends on the specific numerical scheme adopted to discretise the rock formation. In the context of discrete fracture approaches, linear elastic fracture mechanics (LEFM) and cohesive zone model are often employed [275]. The LEFM criteria include the maximum tensile stress criterion, the minimum strain energy density criterion, the maximum principal strain criterion, and the maximum strain energy release criterion [254], among which the maximum tensile stress criterion is the most widely used and can be expressed as:

$$\begin{aligned} \cos \frac{\theta }{2}\left( {{K}_{\text {I}}}{{\cos }^{2}}\frac{\theta }{2}-\frac{3}{2}{{K}_{\text {II}}}\sin \theta \right) \ge {{K}_{\text {Ic}}} \end{aligned}$$

(6)

where ${{K}_{\text {I}}}$, ${{K}_{\text {II}}}$ and ${{K}_{\text {Ic}}}$ are the stress intensity factors for the mode I fracture, the mode II fracture and the fracture toughness respectively, and the propagation direction $\theta$ is determined by

$$\begin{aligned} \begin{aligned}&\tan \left( \frac{\theta }{2} \right) =\frac{1}{4}\left( \frac{{{K}_{\text {I}}}}{{{K}_{\text {II}}}}-\text {sgn} ({{K}_{\text {II}}})\sqrt{{{\left( \frac{{{K}_{\text {I}}}}{{{K}_{\text {II}}}} \right) }^{2}}+8} \right) ,\\&\text {-}\pi<\theta <\pi \end{aligned} \end{aligned}$$

(7)

where sgn() denotes the sign function. The maximum tensile stress criterion was extended to include the effect of ${{{K}_{\text {III}}}}$, the stress intensity factor for mode III fracture, in [281]. In addition, there are also some other variations in the category of LEFM criteria, such as the F-criterion [292].

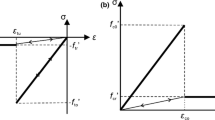
The criteria based on stress intensity factors are generally used when the rock is treated as linear elastic material. The cohesive zone model, first developed by Dugdale [97] and Barenblatt [20], is commonly used to account for non-linear mechanics effects [275]. As shown in Fig. 2a, a process zone ahead of the real fracture is assumed to avoid the singularity near crack tip. In the process zone, a traction-separation law is introduced to define the relationship between fracture width and cohesive traction, which can take different forms [240]. In the simplest case as shown in Fig. 2b, the fracture surfaces begin to separate when the cohesive strength $\sigma _{c}$ (i.e. tensile strength $\sigma _{t}$) is reached, and when the separation reaches a critical value $\delta _{c}$, the traction decreases linearly to zero and the failure occurs [225, 275, 282]. The critical separation $\delta _{c}$ satisfies $G_{c}=\sigma _{t}\delta _{c}/2$. Since the fracture propagation is a natural outcome of the initial-boundary value problem, no external branching criterion is needed to simulate complex fracture network.

Fig. 2

Schematics of cohesive zone model: a definitions of model parameters and b a typical traction-separation law

When simulating fracture propagation with smeared fracture models, the strain threshold and Mohr-Coulomb failure criterion are normally adopted to determine whether or not an element will damage [188]. In phase field model (PFM), the fracture surface energy is combined with the strain energy of rock and solved together, and as a result there is no extra fracture criterion [52, 180, 210]. For discontinuum-based methods, the fracture is represented by the breakage of bonds between particles or blocks, and therefore the corresponding fracture criterion is implicitly determined by the rule of bonds breakage.

2.2 Proppant Transport

The introduction of proppants makes fluid flow inside fracture become a particle-laden flow. The influence of the proppants to the process of hydraulic fracturing are manifold [19]: (1) the change of rheological properties of fracturing fluid; (2) proppant settling and convection; (3) formation and evolution of the proppants bank; (4) screen-out due to the jam of proppants near the fracture tips, etc. More importantly, the distribution of proppant after flow back have a significant influence on the final fracture network. Due to the complexity and significance of the process, it is reviewed separately in [19].

2.3 Leakoff

It has been commonly observed in the petroleum industry that significant leakoff occurs during the process of hydraulic fracturing [16]. The amount of fracturing fluid that gets into the reservoir depends on the properties of formation and fracturing fluid. The leakoff ranges between $10\%\sim50\%$ in brittle formation and $80\%\sim99\%$ in soft formations (e.g. unconsolidated sandstone). Despite the low permeability in tight-shale gas formations, a relative high leakoff ($50\%\sim80\%$) still occurs partially due to the presence of natural fractures [17].

The potential impact of leakoff on hydraulic fracturing treatments has long been recognized [242]. The leakoff has two main effects: (1) it retards the propagation of hydraulic fracture and changes the geometry due to the reduction of fracturing fluid in the fracture; (2) it also contributes to the increase of proppant concentration in the fracture and affects the final distribution of proppant.

An asymptotic solution for crack tip in permeable rocks was presented in [185] which shows a stronger singularity than that in impermeable rocks. Such asymptotic solutions can help to improve the accuracy of numerical simulations [44]. Using the KGD model, the impact of leakoff in a viscosity dominated propagation regime was studied by Adachi and Detournay [5], where the asymptotic solutions with and without leakoff are first derived by using a semi-analytical method and then compared with the transient solutions. The results show that leakoff can change the propagation regime of hydraulic fracturing. More recently, a sensitivity study of leakoff coefficient was conducted by Yao et al. [361] using a 3D pore pressure cohesive element model, and the results show a higher leakoff coefficient leads to a shorter and narrower fracture.

The proppant concentration increases as the fracturing fluid leaks from the fracture into the formation, and it grows more rapidly in the vicinity of crack tip due to higher leakoff rate and smaller fracture width [19, 69, 82]. It was concluded by Daneshy [82] that the increased proppant concentration hinders the proppant settling and is beneficial to the proppant transport. In order to study the effect of leakoff on the proppant transport along the direction of fracture propagation, Sharma and Gadde [289] conducted a numerical simulation with the slip velocity between proppant and fracturing fluid ignored. Their numerical results suggest a high leakoff restricts the spread of proppant along the direction of fracture propagation. Moreover, Smith et al. [306] concluded that leakoff and the heterogeneity of formation can dramatically change the proppant distribution when the fracture shuts in. Another phenomenon resulting from leakoff is screen-out [334]. High leakoff may lead to significant reduction of effective width of flow channel especially near the crack tip, which can then prevent further fracture propagation.

In numerical simulations, leakoff can be modelled in both coupled and uncoupled modes depending on whether or not the pore pressure is simulated for the rock formation [314]. In the uncoupled case, Carter’s leakoff model has been widely used [3, 5, 45, 92, 234, 361], and the leakoff rate is expressed as:

$$\begin{aligned} {{q}_{L}}=2{{S}_{p}}\delta (t-t_{0}(x))+\frac{2{{C}_{L}}}{\sqrt{t-t_{0}(x)}} \end{aligned}$$

(8)

where ${S_{p}}$ is the spurt loss (set to zero in some models), $\delta \left( \right)$ the Dirac delta function, ${t_{0}(x)}$ the time taken to generate the fracture at location x, ${C_{L}}$ the leakoff coefficient. The spurt loss term $2{{S}_{p}}\delta (t-t_{0}(x))$ represents the amount of fluid instantaneously leaking into the porous rock when new fracture surfaces are exposed. Carter’s leakoff coefficient ${C_{L}}$ is related to such factors as the fluid viscosity, formation permeability and filtrate cake formation.

Carter’s leakoff model has been implemented in Elfen tgr [248] with modifications. The spurt loss is simulated over a short time window instead of being added immediately after the new fracture surfaces emerge and the total volume of fluid loss is determined experimentally [339].

The 1D Carter’s leakoff model is independent of the pressure difference between the fracture fluid pressure and the rock formation pore fluid pressure. This drawback was overcome by Abousleiman [1] in an improved model [1, 343]:

$$\begin{aligned} {{q}_{L}}=\frac{2\kappa (\sigma _{0}-p_{0})}{\sqrt{(\pi c(t-t_{0}(x)))}}+\frac{2\kappa }{\sqrt{\pi c}}\int _{t_{0}(x)}^{t}{\frac{\partial p_{n}(x,t')}{\partial t'}\frac{1}{\sqrt{t-t'}}dt'}; \end{aligned}$$

(9)

where $\kappa$ is the mobility coefficient defined as the ratio of the permeability $k_{r}$ to the fluid viscosity $\mu$, c the diffusivity coefficient defined as $c=\kappa /\phi _{r} C_{p}$, $\phi _{r}$ the porosity of the rock, $C_{p}$ the compressibility of the pore and pore fluid system, $\sigma _{0}$ the minimum in-situ stress, $p_{0}$ the in-situ pore pressure, $p_{n}$ the net pressure defined as $p_{n}=p-\sigma _{0}$, and p the fluid pressure in the fracture.

It should be noted that Carter’s leakoff model is derived from the one-dimensional Darcy’s flow taking into account the pore-pressure accumulation, and it is only valid for the single planar fracture with the hydraulic fracture propagating sufficiently faster than the seepage flow inside the formation [179, 354]. If this is not the case, the use of Eq. (8) can lead to overestimation of fracture length [312]. In addition, for multiple hydraulic fractures, the leak off from each fracture all contribute to the increase of the pore pressure in the reservoir, which in turn reduces the leak off flow rate. This process has to be solved in the fully coupled numerical models (e.g. FEM). The leakoff flow rate is determined by the rheological properties of fracturing fluid, local permeability of rock and the pressure difference between the fracturing fluid and the pore pressure inside reservoir [118, 119, 392]. Specifically, in the fully coupled mode, the leakoff flow rate is expressed as:

$$\begin{aligned} {q_{L}}=\frac{k_{r}}{\mu }\frac{\partial p}{\partial n} \end{aligned}$$

(10)

where $k_{r}$ is the rock permeability, $\mu$ is the viscosity of fracturing fluid, and ${\partial p}/{\partial n}$ is the pressure gradient at the fracture surface.

Salimzadeh et al. [271] compared Carter’s leakoff model with a coupled FEM model on the propagation of a penny-shaped hydraulic fracture. The two models are found consistent with each other when the seepage of fluid into rock is restricted to follow the direction perpendicular to the fracture surface. However, in the realistic case where the leakoff flow is in 3D, Carter’s leakoff model underestimates the leakoff flow rate, and overestimates the fracture length and width.

2.4 Poroelastic Effect

A more realistic model for the mechanical behaviour of porous rock formation is provided by the classic theory of poroelasticity [26], where the rock deformation is affected not only by the elastic properties of formation but also by the associated porous media flow conditions. Therefore, taking into account the poroelastic effect of formation, the rock deformation and the porous media flow are coupled as [329]:

$$\begin{aligned}&G{{u}_{i,jj}}+\frac{G}{1-2\upsilon }{{u}_{j,ji}}-\alpha {{P}_{,i}}+{{f}_{i}}=0 \end{aligned}$$

(11)

$$\begin{aligned}&\nabla \left[ \frac{k_{r}}{\mu }\left( \nabla P+\rho_{f} \varvec{g} \right) \right] =S\frac{\partial P}{\partial t}+\alpha \frac{\partial {{\varepsilon }_{v}}}{\partial t}\ \end{aligned}$$

(12)

where G is the shear modulus, $\alpha$ Biot coefficient, ${f_{i}}$ body force, $k_{r}$ the rock permeability, P the pore pressure, $S=1/M$ the storage coefficient (M is the Biot modulus), and ${\varepsilon _{v}}$ the volumetric strain.

Poroelastic effects on hydraulic fracturing are generally deemed to be significant [29]: (1) the distribution of the in-situ pore pressure or the accumulation of pore pressure due to leakoff can alter the mechanical deformations and, thereby, propagation of hydraulic fractures; and (2) the constitutive relation varies from drained condition to undrained condition and the effective stress can be related to the rock failure.

An experimental investigation was conducted by Bruno and Nakagawa [34] to study the influence of pore pressure on the initiation and propagation of tensile fractures, and their results suggest that in the absence of far-field stress difference, a hydraulic fracture tends to propagate to the regions of higher local pore pressure.

Berchenko and Detournay [24] analytically computed the stress field in a 2D domain with an injection well and pumping well, and then they studied the hydraulic fracture propagation under the effect of these two wells using the displacement discontinuity method (DDM). The analytical and numerical results suggest the hydraulic fracture is attracted by the pore pressure, which agrees with the experimental results in [34]. The numerical simulation performed by Ji et al. [157] demonstrates higher effective stress coefficient, i.e. stronger poroelastic effect, contributes to shorter and narrower fracture and a higher propagation pressure is also needed due to the so-called “back stress” effect. Rock failure around hydraulic fractures in poroelastic rock is analysed in [119, 258]. The effect of pore pressure field on the propagation of tensile fracture is studied in [324] through numerical simulation. Their fracture trajectory prediction agrees well with the experimental result from [34], and it is concluded that both the magnitude and gradient of pore pressure influence the fracture propagation. More recently, the poroelastic effect has been comprehensively considered in 3D modelling of hydraulic fracturing [175, 239, 271].

2.5 Interaction of Hydraulic and Natural Fractures

Widely detected in shale formation [110], natural fractures influence the hydraulic fracturing treatment in various ways including the stimulated fracture pattern, leakoff, and the proppant transport etc. Natural fractures are an important source for non-planar and multistranded hydraulic fractures [259, 331], because some natural fractures may be reactivated or crossed during the propagation of hydraulic fracture, forming a complex fracture network instead of a planar fracture. Due to the significant impact of natural fractures on the hydraulic fracturing treatment, they have been extensively studied through field trials, experimental tests, and analytical and numerical investigations [80, 108, 170, 287, 333].

The mineback experiments at the U.S. DOE Nevada Test Site [331] exposed the interaction between hydraulic and natural fractures. Even in the most homogeneous tuff formation, hydraulic fractures are observed to be non-planar and multistranded. Hydraulic fracture is normally offset by the joints, and sometimes two or more fractures initiate from these offsets. In addition, the hydraulic fracture may also terminate near faults or propagate across with a changed orientation. This complex propagation pattern has a significant impact on the fracturing pressure and proppant transport. Another field investigation related to natural fractures was conducted in Barnett Shale [109], where the reactivation of natural fractures during the hydraulic fracturing treatment is detected through microseismic monitoring. Therefore, characterization of the natural fracture system and the in-situ stress measurement are both essential for the design and optimization of a hydraulic fracturing treatment.

The interaction between hydraulic and natural fractures has also been studied using tri-axial experiments [25, 84, 100, 133, 197, 390]. To mimic the natural fractures, Beugelsdijk et al. [25] and De Pater and Beugelsdijk [84] used overdried rock blocks with shrinkage cracks to conduct the experiments of hydraulic fracturing. A sensitivity analysis for injection flow rate, viscosity and stress regime are performed, and the experimental results show: (1) higher flow rate and viscosity reduce the tortuosity of hydraulic fracture and (2) discontinuities with larger aperture have a more significant impact on hydraulic fracture propagation. Synthetic materials have also been used as test samples in experimental investigations [100, 197, 390], where “natural fractures” are added artificially. The test results suggest: (1) hydraulic fracture normally crosses small-aperture natural fractures and dilates large-aperture natural fractures, (2) natural fractures and horizontal differential stress are the main geological factors which influence hydraulic fracture propagation, and (3) higher natural fracture density and higher injection flow rate lead to higher treatment pressure.

More recently, CT-scan techniques have been increasingly used in experiments to detect natural fractures and stimulated hydraulic fracture network [40, 125, 162, 196, 198, 397]. Liu et al. [196] identified 3D propagation and distribution of hydraulic fractures in heterogeneous rocks and found the rock heterogeneity and horizontal in situ stress ratio have a significant influence on the stimulated fracture network. Luo et al. [198] conducted CT-scan on carbonate rock specimens before and after the hydraulic fracturing to investigate the shear slippage behaviour of the natural fractures. The natural fractures identified with CT-scan in experiments typically show much more complex geometries than those considered in numerical simulation [40, 396].

The aforementioned field and lab tests both suggest that the fracture pattern resulting from the interaction between hydraulic and natural fractures depends on a range of geological and operational factors, such as the in-situ stress, the intersection angle, the shear strength of natural fracture, and the injection flow rate. As shown in Figs. 3 and 4, different scenarios can occur when a hydraulic fracture intersects with natural fractures, they include arrest, crossing, penetration and offset [60, 78, 129, 373]. More complex scenarios may happen when the basic modes mix with each other. For example, penetration may also happens after crossing.

Fig. 3

A hydraulic fracture approaching to a natural fracture

Fig. 4

Intersection between hydraulic and natural fractures

Analytical models have been developed to estimate how a hydraulic fracture behaves when intersecting with a natural fracture for specific geological conditions and treatment parameters. Potluri et al. [243] reviewed three analytical fracture interaction criteria developed by Blanton [27], Warpinski and Teufel [331] and Renshaw and Pollard [262], respectively. Blanton [27] assumed that crossing occurs when pressure required for re-initiation is lower than that required for opening the natural fracture. Hence, zero-cohesion is set for the natural fractures in this model. Both Warpinski and Teufel [331] and Renshaw and Pollard [262] estimated the occurrence of crossing based on the criterion for shear slippage of natural fractures. The model proposed by Renshaw and Pollard [262] is specially designed for orthogonal intersection between hydraulic and natural fractures, and it has been further extended to general cases with arbitrary intersection angles [128, 129]. Specifically, normal and shear stresses on natural fractures are computed according to the stress field around crack tip, after which they are used to check whether or not slip occurs for a natural fracture with specific coefficient of friction and interface cohesion. If no slip occurs, the hydraulic fracture will cross the natural fracture, otherwise it will be arrested or penetrate into the natural fracture. With respect to the horizontal principle stress ratio/difference and the coefficient of friction, a group of solution curves for different intersection angles are obtained, and each divides the 2D parameter space into two regions: one for crossing and the other for arrest and penetration.

Numerical simulations have also been performed to study the interaction of hydraulic fracture and a single natural fracture [268, 373, 383]. Zhang and Jeffrey [373] investigated the effect of natural fracture friction and secondary flaws on the penetration and re-initiation of hydraulic fracture. The numerical results show that it is difficult for the hydraulic fracture to penetrate into the natural fracture with weak friction, and the competition between crack re-initiation and penetration plays an important role in fracture propagation when secondary flaws exist. This model was also used to investigate the behaviour of hydraulic fracture with simple network geometries [378]. Dahi-Taleghani and Olson [78] enriched the fracture propagation criterion in LEFM to estimate whether the hydraulic fracture will cross the natural fracture or penetrate into it. Once the hydraulic fracture encounters with a natural fracture, the relative energy release rate is computed for possible path and the hydraulic fracture will propagate to the path with the highest relative energy release rate. The numerical results confirm that the hydraulic fracture exerts large tensile and shear stresses ahead of and near the tip, which may be large enough to open natural fractures and the stress anisotropy can enhance the effect of natural fractures on hydraulic fracture propagation. Zhang and Ghassemi [383] investigated the interaction between hydraulic and natural fractures by using the virtual multidimensional internal bond (VMIB) method. It is found that the influence of natural fractures depends on its shear stiffness, inclination and distance to the hydraulic fracture. A hydraulic fracture is prone to be arrested at the natural fracture with low shear stiffness, and is prone to penetrate into the natural fracture with high shear stiffness. Zhao and Young [389] conducted a series of numerical test with different intersection angles and differential stresses using the Particle Flow Code (PFC) 2D. The numerical results show good agreement with the laboratory and field observations and suggest possible mechanisms for interaction between hydraulic and natural fractures. Similar studies were also carried out by Zangeneh et al. [365] and Zou et al. [396], both using the block-based DEM and the numerical results also match well with existing experimental results. Using FEM, Rahman and Rahman [256] investigated the effect of natural fracture length and approach angle on the interaction between hydraulic and natural fractures.

The effect of natural fracture network on the hydraulic fracturing is more interesting to the engineering applications and has been extensively investigated numerically [84, 317, 384]. De Pater and Beugelsdijk [84] investigated the propagation of hydraulic fracture in a naturally fractured reservoir with a 2D discrete element model. The simulation shows that high flow rate or viscosity drives hydraulic fractures while low flow rate leads to excessive leakage of fracturing fluid into the natural fracture network. Using DDM, Olson and Taleghani [230] investigated interaction between multiple hydraulic fractures from a horizontal wellbore (or a single hydraulic fracture from a vertical wellbore) and natural fractures with the specific orientation in 2D space. It is concluded from the numerical results that the existence of natural fractures leads to more complex fracture networks in case of higher injection pressure and lower stress anisotropy. Dershowitz et al. [87] investigated the effect of natural fracture network in 3D space using the so-called Discrete Fracture Network (DFN) approach. Despite some limitations such as idealised shape and orientation of natural fractures, this approach explicitly models the interaction between hydraulic and natural fractures and can be compared with the results from Elfen tgr. This model was also used by McLennan et al. [203] and Vishkai et al. [315] with some improvements. Weng et al. [335] developed a simulator named unconventional fracture model (UFM) to simulate the 3D propagation of hydraulic fracture in naturally fractured reservoir by using enhanced 2D DDM. All hydraulic and natural fractures are assumed to be vertical and the width and height are computed according to Pseudo-3D model. The analytical crossing criterion in [128, 129] is incorporated. It is concluded that low stress anisotropy and interfacial friction lead to more complex fracture network. The model was also applied in [174, 336, 359]. Fu et al. [106] developed a 2D explicitly coupled hydro-mechanical model based on FEM to simulate hydraulic fracturing in discrete fracture network. Effect of anisotropic horizontal stress on the final fracture network is investigated. More recently, Settgast et al. [286] and Huang et al. [150] developed a 3D model to simulate the interaction between one main hydraulic fracture and vertical natural fractures perpendicular or parallel to the hydraulic fracture. Dahi Taleghani and Olson [79] simulated the propagation of hydraulic fracture in a 2D naturally fractured reservoir using XFEM. The effect of differential stress, natural fractures orientations and cement bonding strength on the stimulated fracture network is investigated. Zhang et al. [384] simulated the hydraulic fracture propagation in a reservoir with two sets of natural fractures using DDM. A dimensionless parameter dependent on the injection flow rate, viscosity, elastic modulus and toughness of rock is proposed to describe the competition between viscosity dissipation of fluid and the strength of rock deformation, and it is related to the complexity of stimulated fracture network.

More recently, realistic natural fracture geometries have been incorporated into laboratory-scale and field-scale modelling of hydraulic fracturing. Propagation of hydraulic fractures in glutenite, a typical heterogeneous rock with natural fractures, was investigated by Li et al. [187] and Ju et al. [160] using continuum-based discrete element method (CDEM) with the natural fractures and heterogeneities captured through CT-scan. Chen et al. [54] used scanning electron microscope to extract the existing joints from a coal sample and investigated the influences of joints on the propagation of hydraulic fracture. Using PFM, Chen et al. [52] simulated 2D propagation of hydraulic fracture in a natural fracture network mapped from realistic outcrop at field. However, the construction of field-scale subsurface natural fracture network faces complex uncertainties since the relevant information provided by wellbore logs are limited. The information from micro-seismicity and other in situ monitoring techniques can be useful to improve the understanding of stimulated hydraulic fracture networks.

2.6 Heterogeneity, Anisotropy and Bedding Planes of Shale Rock

Along with natural fractures, heterogeneity and anisotropy of the shale rock as well as bedding planes are other sources of the non-planar and multistranded hydraulic fractures. The shale rock formation is widely recognized to be heterogeneous at different scales [99]. But constrained by the computing power and the geological information available, the numerical simulators of hydraulic fracturing often ignore the effects of heterogeneity or simply uses overly simplified models to describe the heterogeneous formation. Specifically, Weibull distribution is commonly adopted to describe the rock properties [358]:

$$\begin{aligned} f(\varTheta )={\frac{m}{{{\varTheta }_{0}}}}{{\left( \frac{\varTheta }{{{\varTheta }_{0}}} \right) }^{m-1}}{exp}{{{\left( -\frac{\varTheta }{{{\varTheta }_{0}}} \right) }^{m}}} \end{aligned}$$

(13)

where $\varTheta$ is the media property, $\varTheta _{0}$ is the scale parameter related to the average value, and m is the homogeneity index.

Different degrees of heterogeneity can be introduced into hydraulic fracturing simulation to model the heterogeneous rock formation [323, 358], and the hydraulic fracture paths can differ greatly between the homogeneous and heterogeneous cases. With the increase of heterogeneity, the hydraulic fracture path becomes more irregular, which is also observed in a 3D simulation by Li et al. [188]. By using an adaptive finite element PFM, Lee et al. [180] simulated the intersection of two perpendicular pressure-driven fractures in rock media with homogeneous and heterogeneous elastic modulus. A smooth fracture surface is predicted in the case of homogeneous rock while an irregular fracture is obtained for the heterogeneous formation.

As a kind of sedimentary rock, the shale rock generally has anisotropic mechanical properties and often contains abundant bedding planes [47, 307, 364]. It is proved experimentally that the rock anisotropy and bedding planes have significant influences on the breakdown pressure and stimulated fractures [192, 288, 319]. Zhang et al. [377] simulated the propagation of a hydraulic fracture perpendicular to a bedding plane using DDM. Depending on the stress conditions, the hydraulic fracture may reinitiate or terminate at the bedding plane. More recently, the influence of bedding planes with different mechanical properties and intersection angles with a hydraulic fracture is systematically investigated using numerical simulation [121, 163]. The numerical results indicate that the bedding planes contribute to the complexity of stimulated fracture network [346].

3 Historical Development of Hydraulic Fracturing Models

Numerous hydraulic fracturing models have been developed to improve the design of hydraulic fracturing treatment and the understanding of specific physical mechanisms. Despite the complex nature of hydraulic fracturing, a significant progress has been made over the past decades through the integration of theory (e.g., LEFM and fluid mechanics), field and lab testing and numerical modelling. In this section, we mainly focus on the classical models developed in early years, which simplify the fracture geometry to varying degrees. The latest hydraulic fracturing models, which are largely motivated by numerical studies, are reviewed in Sect. 4.

3.1 PKN Model

The PKN model came from the pioneering work by Perkins and Kern [242] and Nordgren [226]. Figure 5 provides a schematic illustration for the PKN model, where the problem was simplified by some strict assumptions to make it tractable.

Fig. 5

The PKN model: a the model setup [3] and b the plane strain assumption on vertical section

The governing equations in [226] are analysed here. For the rock deformation, the height of hydraulic fracture is assumed to be constant along the fracture propagation direction and the fracture length is much greater than the height. The aperture profile at any vertical section is restricted to be elliptical and is computed based on the plane strain assumption:

$$\begin{aligned} w=\frac{(1-\nu )}{G}\sqrt{({{h}^{2}}-4{{z}^{2}})}({{p}}-{{\sigma }_{0}}) \end{aligned}$$

(14)

where h is the fracture height, z is the coordinate in vertical direction, p is fluid pressure and ${\sigma _{0}}$ is the confining stress. In this case, the fracture width is only related to the local pressure and the non-local character of the elastic response is neglected. With these assumptions, the elastic equation is equivalent to the equilibrium Eq. (2). The pressure gradient along the fracture propagation direction is computed according to the classic solution for laminar flow in an elliptical tube:

$$\begin{aligned} \frac{\partial {p}}{\partial x}=-\frac{64\mu q}{\pi w_{\max }^{3}h} \end{aligned}$$

(15)

where ${w_{max}}$ is the fracture width at centre. The continuity equation for fluid flow is expressed as:

$$\begin{aligned} \frac{\partial A}{\partial t}+\frac{\partial q}{\partial x}+{{q}_{L}}=0 \end{aligned}$$

(16)

where A is the cross-sectional area of the fracture.

As shown in the above governing equations, the capacity of rock to resist fracture, which is normally described by toughness or strain energy release rate, is not involved in this model. According to Eq. (14), the displacement boundary condition at leading edge of fracture results in a zero pressure difference ${p}-{\sigma _{0}}=0$, and this is often used to detect fracture in this model. The above three equations were solved in a dimensionless manner by Nordgren [226], along with the displacement boundary condition at fracture leading edge and the constant injection flow rate at injection point. Regardless of the strong assumptions made in the PKN model, it does present a clearly structured modelling framework for hydraulic fracturing, which includes the elasticity equation, the fluid flow equation and the continuity equation, and can capture some key features of the dynamic propagation of hydraulic fracture. An improved PKN model was developed in [91] with the poroelastic effect considered.

3.2 KGD Model

Based on the work by Khristianovic and Zheltov [166], Geertsma and De Klerk [117] developed a well-known hydraulic fracturing model, namely the KGD model. Different from the PKN model, a plane strain condition is applied on the horizontal section as shown in Fig. 6. The KGD model is further developed by Carbonell et al. [42], where the plane strain condition from the original KGD model is reserved, but some corrections are made to the governing equations with more rigorous solution methods. The improved KGD model is explained in detail in this section.

Fig. 6

The KGD model: a the model setup [3] and b the plane strain assumption on the horizontal section

The rock deformation is computed according to an elastic singular integral equation relating the net pressure $p_{n}=p-{\sigma _{0}}$ to the fracture width [48, 114, 178]:

$$\begin{aligned} w=\frac{1}{{{E}'}}\int _{0}^{l}{G\left( \frac{x}{l},\frac{s}{l} \right) }p_{n}ds \end{aligned}$$

(17)

and if an existing fluid lag is present with zero pressure [115]:

$$\begin{aligned} w=\frac{1}{{{E}'}}\int _{0}^{{{l}_{f}}}{G\left( \frac{x}{l},\frac{s}{l} \right) }p_{n}ds-\frac{{{\sigma }_{0}}}{{{E}'}}\int _{{{l}_{f}}}^{l}{G\left( \frac{x}{l},\frac{s}{l} \right) }ds \end{aligned}$$

(18)

where ${E}'=E/(1-{{\nu }^{2}})$ is the plane strain modulus, l is half length of the fracture, ${l_{f}}$ is half length of fluid channel and the integral kernel G is expressed as

$$\begin{aligned} G(\xi ,\eta )=\frac{4}{\pi }{\text {In}}\left| \frac{\sqrt{1-{{\xi }^{2}}}+\sqrt{1-{{\eta }^{2}}}}{\sqrt{1-{{\xi }^{2}}}-\sqrt{1-{{\eta }^{2}}}} \right| \end{aligned}$$

(19)

An inverse relation expressing the net pressure $p_{n}$ by w is used in some other literatures [5, 42, 149] for the case without a fluid lag:

$$\begin{aligned} p_{n}=-\frac{{{E}'}}{4\pi }\int _{-l}^{l}{\frac{\partial w}{\partial s}\frac{ds}{s-x}} \end{aligned}$$

(20)

The corresponding boundary condition is zero fracture width at crack tips.

The fluid flow is governed by Poiseuille’s law (3) and the continuity equation, Eq. (4). Besides the elastic equation, Poiseuille’s law and the continuity equation, a fracture propagation criterion is still needed to control the propagation of hydraulic fracture. Different from the condition of smooth closing in the original KGD model, the LEFM theory is introduced into the model. It is assumed that the hydraulic fracture always propagates in mobile equilibrium which means the mode I stress intensity factor needs to be equal to the rock toughness ${K_{Ic}}$. The propagation condition ${K_{I}=K_{Ic}}$ implies a tip asymptote of fracture width

$$\begin{aligned} w=4\sqrt{\frac{2}{\pi }}\frac{{{K}_{I}}}{{{E}'}}{{(l-x)}^{1/2}}\text { (}l-x\ll l\text {)} \end{aligned}$$

(21)

Alternatively, the propagation condition can also be implemented by computing the mode I stress intensity factor from fluid pressure distribution and fracture length. By using Bueckne-Rice function

$$\begin{aligned} {{K}_{I}}=2\sqrt{\frac{l}{\pi }}\int _{0}^{l}{\frac{p_{n}}{\sqrt{{{l}^{2}}-{{x}^{2}}}}}dx \end{aligned}$$

(22)

If a fluid lag with zero pressure exists, $K_{I}$ is computed piecewise

$$\begin{aligned} {{K}_{I}}=2\sqrt{\frac{l}{\pi }}\left( \int _{0}^{{{l}_{f}}}{\frac{p_{n}}{\sqrt{{{l}^{2}}-{{x}^{2}}}}}dx+\int _{{{l}_{f}}}^{l}{\frac{-{{\sigma }_{0}}}{\sqrt{{{l}^{2}}-{{x}^{2}}}}}dx \right) \end{aligned}$$

(23)

Since the pioneering work by Spence and Sharp [308], Savitski and Detournay [276], and Detournay [89], scaling has been widely adopted as an indispensable step in deducing analytical solutions for hydraulic fracturing to transfer the governing equations into dimensionless forms. A common form of scaling can be expressed as:

$$\begin{aligned} \begin{aligned}&l(t)=L\gamma \\&p_{n}(x,t)=\epsilon {E}'\varPi \\&w(x,t)=\epsilon L\varOmega \\ \end{aligned} \end{aligned}$$

(24)

where L is a length scale, $\epsilon$ is a small factor, $\xi$, $\gamma$, $\varPi$ and $\varOmega$ are normalized coordinate along fracture, normalized fracture length, normalized net-pressure and normalized fracture width, respectively.

Introducing the scaling Eq. (24) into the governing equations results in a set of normalized governing equations:

$\circ$:

Normalised elastic equation

$$\begin{aligned} \frac{\varOmega }{\gamma }=\int _{0}^{{{\xi }_{\text {f}}}}{G\left( \xi ,{\xi }' \right) }\varPi \left( {\xi }',t \right) d{\xi }'-{\mathcal {T}}\int _{{{\xi }_{\text {f}}}}^{1}{G\left( \xi ,{\xi }' \right) }d{\xi }', \xi \in (0,1) \end{aligned}$$

(25)

$\circ$:

Normalised Poiseuille’s law

$$\begin{aligned} \begin{aligned}&{{\mathcal {G}}_{v}}\left[ \left( \frac{t{\dot{\gamma }}}{\gamma }+\frac{t{\dot{\varepsilon }}}{\varepsilon }+2\frac{t{\dot{L}}}{L} \right) \int _{\xi }^{{{\xi }_{f}}}{\varOmega d\xi }\text {+t}{{\varOmega }_{f}}{{{{\dot{\xi }}}}_{f}}+\varOmega \xi \left( \frac{t\dot{\gamma }}{\gamma }+\frac{t{\dot{L}}}{L} \right) \right. \\&\quad \left. +\int _{\xi }^{{{\xi }_{f}}}{t{\dot{\varOmega }}d\xi } \right] \text {+}{{\mathcal {G}}_{c}}\int _{\xi }^{{{\xi }_{f}}}{\Gamma d\xi }=-\frac{1}{{{\mathcal {G}}_{m}}}\frac{{{\varOmega }^{3}}}{{{\gamma }^{2}}}\frac{\partial \varPi }{\partial \xi },\text { }\xi \in (0,{{\xi }_{f}}) \end{aligned} \end{aligned}$$

(26)

where $\Gamma =1/\sqrt{1-\theta (\xi )}$, $\theta (\xi )={{t}_{0}}/t$ is the normalized arrival time of fluid front remaining to be determined. The corresponding boundary condition in the lag is

$$\begin{aligned} \varPi =-{\mathcal {T}},\text { }\xi \in \text { }\!\![\!\!\text { }{{\xi }_{f}}\text {,1 }\!\!]\!\!\text { } \end{aligned}$$

(27)

$\circ$:

Global continuity equation

$$\begin{aligned} \frac{1}{2\gamma }={{\mathcal {G}}_{v}}\int _{0}^{{{\xi }_{f}}}{\varOmega }d\xi +2{{\mathcal {G}}_{c}}\int _{0}^{{{\xi }_{f}}}{\sqrt{1-\theta (\xi )}}d\xi \end{aligned}$$

(28)

$\circ$:

Fracture propagation criterion

$$\begin{aligned} {{\mathcal {G}}_{k}}=\frac{{{2}^{7/2}}}{\pi }{{\gamma }^{1/2}}\left( \int _{0}^{{{\xi }_{f}}}{\frac{\varPi d\xi }{\sqrt{1-{{\xi }^{2}}}}}-{\mathcal {T}}\arccos {{\xi }_{f}} \right) \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned}&{{\mathcal {G}}_{v}}=\frac{\varepsilon {{L}^{2}}}{{{Q}_{0}}t}, {{\mathcal {G}}_{c}}=\frac{{C}'L}{{{Q}_{0}}{{t}^{1/2}}}, {{\mathcal {G}}_{m}}=\frac{{{Q}_{0}}{\mu }'}{{{\varepsilon }^{4}}{{L}^{2}}{E}'} \\&{{\mathcal {G}}_{k}}=\frac{{{K}'}}{\varepsilon {E}'{{L}^{1/2}}}, {\mathcal {T}}=\frac{{{\sigma }_{0}}}{\varepsilon {E}'} \end{aligned} \end{aligned}$$

(30)

in which ${{\xi }_{f}}={{l}_{f}}/l$ is the fluid fraction, the small factor $\epsilon$ and the length scale L are still to be determined according to the specific propagation regimes to be solved, and ${E}'=\frac{E}{1-{{\nu }^{2}}},\text { }{\mu }'=12\mu ,\text { }{C}'=2{{C}_{L}},\text { }{K}'=\frac{8}{\sqrt{2\pi }}{{K}_{Ic}}$.

The dimensionless parameters can be divided into three groups: (1) ${\mathcal {G}}_{m}$ and ${\mathcal {G}}_{k}$; (2) ${\mathcal {T}}$ and (3) ${\mathcal {G}}_{v}$ and ${\mathcal {G}}_{c}$. The factors ${\mathcal {G}}_{m}$ and ${\mathcal {G}}_{k}$ reflect the energy dissipated on driving viscous fluid and fracturing rock while the factors ${\mathcal {G}}_{v}$ and ${\mathcal {G}}_{c}$ reflect whether the fluid storage or leakoff dominates the hydraulic fracturing process. In order to analyse how the input parameters influence hydraulic fracturing behaviours through dimensionless parameters, explicit expressions of dimensionless parameters need to be determined. Without loss of generality, we restrict ${\mathcal {G}}_{m}=1$ and ${\mathcal {G}}_{v}=1$. After solving the scaling parameters L and $\epsilon$, the other three dimensionless parameters can be expressed as:

$$\begin{aligned} \begin{aligned}&{\mathcal {K}}={{G}_{k}}={K}'{{\left( \frac{1}{{{Q}_{0}}{{{{E}'}}^{3}}{\mu }'} \right) }^{1/4}}, {\mathcal {T}}={{\sigma }_{0}}{{\left( \frac{t}{{{{{E}'}}^{2}}{\mu }'} \right) }^{1/3}}, \\&{\mathcal {L}}={{G}_{c}}={C}'{{\left( \frac{{E}'t}{{\mu }'Q_{0}^{3}} \right) }^{1/6}} \\ \end{aligned} \end{aligned}$$

(31)

With the propagation of hydraulic fracture, the time-independent dimensionless toughness ${\mathcal {K}}$ remains unchanged while the dimensionless confining stress and dimensionless leakoff increase as a power function of time. The dimensionless confining stress and dimensionless leakoff coefficient can be rewritten as:

$$\begin{aligned} {\mathcal {T}}= & {} {{\sigma }_{0}}{{\left( \frac{t}{{{{{E}'}}^{2}}{\mu }'} \right) }^{1/3}}={{\left( \frac{t}{{{t}_{om}}} \right) }^{1/3}} \end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {L}}= & {} {C}'{{\left( \frac{{E}'t}{{\mu }'{{Q}_{0}}^{3}} \right) }^{1/6}}={{\left( \frac{t}{{{t}_{m{\tilde{m}}}}} \right) }^{1/6}} \end{aligned}$$

(33)

where the corresponding time scales ${t_{om}}$ and ${t_{mm}}$ are determined by:

$$\begin{aligned} {{t}_{om}}=\frac{{{{{E}'}}^{2}}{\mu }'}{\sigma _{0}^{3}}\text {, }{{t}_{m{\tilde{m}}}}=\frac{{\mu }'{{Q}_{0}}^{3}}{{E}'{{{{C}'}}^{6}}} \end{aligned}$$

(34)

The three dimensionless parameters range from 0 to $\infty$, and they involve all relevant physical parameters and constitute a 3D parametric space. A wedge-shaped parametric space, shown in Fig. 7a, has been constructed considering the convergence of early time (${\mathcal {T}}\ll 1$) and late time (${\mathcal {T}}\gg 1$) solutions for large dimensionless toughness [2]. The parametric space plays a critical role in deriving analytical solutions in limiting cases and guiding the numerical simulation.

Fig. 7

Parametric space of plane strain hydraulic fracturing and limiting propagation regimes [49]

As an example, the derivation of the self-similar solution for the OK edge is described here. As there is no leakoff in this case, ${\mathcal {G}}_{m}$ and ${\mathcal {G}}_{v}$ are set to 1. The other three dimensionless parameters are listed in Eq. (31). Since $t=0$, ${\mathcal {T}}=0$ and ${\mathcal {L}}=0$. The normalised governing equations turn into:

$\circ$:

Normalised elastic equation

$$\begin{aligned} {\bar{\varOmega }}=\int _{0}^{{{\xi }_{f}}}{G(\xi ,{\xi }')}\varPi ({\xi }',t)d{\xi }' \end{aligned}$$

(35)

$\circ$:

Normalised Poiseuille’s law

$$\begin{aligned} \int _{\xi }^{{{\xi }_{f}}}{{{\bar{\varOmega }}}}d\xi +\frac{2}{3}\xi {\bar{\varOmega }}=-{{{\bar{\varOmega }}}^{3}}\frac{\partial \varPi }{\partial \xi },\text { }\varPi ({{\xi }_{f}})=0 \end{aligned}$$

(36)

$\circ$:

Global continuity equation

$$\begin{aligned} 2{{\gamma }^{2}}\int _{0}^{{{\xi }_{f}}}{{{\bar{\varOmega }}}}d\xi =1 \end{aligned}$$

(37)

$\circ$:

Fracture propagation criterion

$$\begin{aligned} {\mathcal {K}}=\frac{{{2}^{7/2}}}{\pi }{{\gamma }^{1/2}}\int _{0}^{{{\xi }_{f}}}{\frac{\varPi d\xi }{\sqrt{1-{{\xi }^{2}}}}} \end{aligned}$$

(38)

or

$$\begin{aligned} 1-\xi \ll 1:{\bar{\varOmega }}={\mathcal {K}}{{\gamma }^{-1/2}}{{(1-\xi )}^{1/2}} \end{aligned}$$

(39)

Instead of solving the fluid fraction $\xi _{f}$ as an unknown for specific dimensionless toughness, a value of $\xi _{f}$ is postulated first with the corresponding dimensionless toughness computed later. As for a given fluid fraction, the normalised elastic equation and Poiseuille’s law can be solved independently of the continuity equation and the fracture propagation criterion. Newton iteration procedure is adopted to solve the piecewise linear profile of the dimensionless net pressure and the corresponding dimensionless fracture width. Once the dimensionless fracture width and the net-pressure are computed, the dimensionless fracture length and the toughness are computed according to Eqs. (37) and (38), respectively. By using this procedure, a series of solutions correspond to different fluid fraction can be solved along the OK edge [115].

Using similar approaches, asymptotic or transient solutions can be obtained on other vertices, edges and surfaces in the parametric solution space of Fig. 7. Table 1 provides a summary for existing analytical solutions to the KGD model.

Table 1 (Semi-)Analytical solutions for the KGD model

Besides the semi-analytical solutions for the whole fracture, the behaviour of hydraulic fracture close to the crack tip under different propagation regimes has also been studied. Desroches et al. [88] derived the analytical solutions of fracture width and fluid pressure in the vicinity of crack tip for hydraulic fracture in an impermeable linear elastic formation. The fluid front is assumed to coincide with crack tip and the hydraulic fracture propagates in a viscosity-dominated regime. The singularity at crack tip for fracture width and fluid pressure are $2/(n+2)$ and $-n/(n+2)$ respectively for the power-law fluid (n is the power law index) and 2/3 and $-1/3$ for Newtonian fluid. This work was extended by Lenoach [185] to the case of permeable rocks by simulating the leakoff using Carter’s leakoff model and it shows a slightly stronger singularity. The crack-tip solutions for arbitrary dimensionless toughness was numerically solved in [113], where a fluid lag with unknown length needs to be determined and the singular solution at crack tip for fracture width decreases from 3/2 for a zero dimensionless toughness to 1/2 for a large dimensionless toughness. Later, exchange of pore pressure between fluid lag and porous media was considered by Detournay and Garagash [90]. Although these analytical solutions are limited to the crack tip area, they can be used as enriched functions for tip element in numerical simulation or benchmark to verify the numerical results obtained under similar conditions.

Fig. 8

The radial model [3]

3.3 Radial Model

When the wellbore is along the direction of the minimum principal stress, penny-shaped hydraulic fracture perpendicular to the wellbore direction is prone to form, as shown in Fig. 8. Geertsma and De Klerk [117] proposed the radial model for this case. A similar set of governing equations as the KGD model are used with the plane strain assumption replaced by the axisymmetric assumption. The penny-shaped hydraulic fracture is assumed to propagate in an infinite linear elastic media with confining stress. The original radial model has been further improved by a series of subsequent works [37, 89, 276, 308]. Since the governing equations of the radial model share the same structure as the KGD model, a similar parametric solution space has also been constructed.

Savitski and Detournay [276] solved the self-similar zeros-toughness solution (exact solution at the M vertex) and the first-order asymptotic solution for large-toughness case (the K vertex). As for the MK-edge solutions, they are no longer self-similar since either the dimensionless toughness or viscosity become time-related terms. A series of numerical solutions at MK-edge have been obtained by using the code Loramec and are compared with the zeros-toughness and first-order asymptotic solution for the large-toughness case. These results and conclusions were discussed by Detournay [89]. Bunger and Detournay [35] investigated toughness-dominated propagation of penny-shaped hydraulic fracture with leakoff by using the procedure explained in Sect. 3.2 ($\tilde{\text {K}}$ vertex and K$\tilde{\text {K}}$ edge). The asymptotic solutions for K vertex and $\tilde{\text {K}}$ vertex are solved in a semi-analytical way while the transient solution for K$\tilde{\text {K}}$ edge is solved numerically and shows good agreement with the asymptotic K-vertex and $\tilde{\text {K}}$ vertex solutions. Bunger and Detournay [36] solved the small-time asymptotic solution (near O vertex) using a similar scheme.

Fig. 9

A penny-shaped hydraulic fracture propagating parallel to a free surface in semi-infinite medium

For applications in the oil and gas industry, the hydraulic fracture is often assumed to propagate in an infinite space. For other applications, such as environmental remediation [221] and rock excavation [375], a free surface is often present near the hydraulic fracture, as shown in Fig. 9. A penny-shaped hydraulic fracture model with the presence of free surface was developed by Zhang et al. [375], and the governing equations are listed below:

$\circ$:

Elastic equation

The non-local elasticity relation between fracture width and fluid pressure is described using DDM and expressed as

$$\begin{aligned} {\mathcal {D}}\left\{ \frac{w}{R};\frac{R}{H} \right\} =\frac{p}{{{E}'}} \end{aligned}$$

(40)

where ${\mathcal {D}}$ is the linear functional based on DDM, and R is the fracture radius.

$\circ$:

Poiseuille’s law

$$\begin{aligned} q=-\frac{{{w}^{3}}}{12\mu }\frac{\partial p}{\partial r} \end{aligned}$$

(41)

$\circ$:

Continuity equation Without leakoff, the continuity equation is given as

$$\begin{aligned} \frac{\partial w}{\partial t}+\frac{1}{r}\frac{\partial (rq)}{\partial r}=0 \end{aligned}$$

(42)

$\circ$:

Fracture propagation criterion

$$\begin{aligned} w\simeq \frac{{{K}'}}{{{E}'}}{{(R-r)}^{1/2}}\text { (}R-r\ll R\text {)} \end{aligned}$$

(43)

These governing equations are transferred into two different normalized forms depending on the scaling system used (viscosity scaling system or toughness scaling system). Both zero-toughness and zero-viscosity solutions can be obtained, and the relation between the dimensionless results and the ratio R/H are investigated.

Zhang et al. [376] solved a more general solution numerically using the same governing equations. The numerical solutions are validated by two self-similar solutions: (1) early time solution at OK edge, i.e. deep buried crack with zero confining stress; and (2) large time solution at $\tilde{\text {K}}$ vertex. A parametric space similar to Fig. 7a is constructed but the $\tilde{\text {K}}\tilde{\text {M}}\tilde{\text {O}}$ plane represents the limitation of very small R/H instead of infinite leakoff [122, 376]. Another model was developed by Bunger and Detournay [35] and it adopts classical plate theory to compute the relation between fracture width and fluid pressure. A large R/H asymptotic solution is solved in the condition of zero-viscosity.

Fig. 10

The Pseudo 3D (P3D) model: a the cell-based model and b the lumped elliptical model

3.4 Pseudo 3D (P3D) Model

As discussed in Sect. 3.1, the PKN model has two apparent limitations: (1) the fracture height is assumed to be constant along the fracture propagation direction; (2) the non-local elastic response is ignored. The removal of the first limitation leads to the development of cell-based P3D model, as shown in Fig. 10a. An early work in this direction was presented by Simonson et al. [304], where the influences of different material properties, in-situ stress variations and pressure gradient on the containment of hydraulic fracture are investigated by using a three-layer 2D model combined with the LEFM theory. It is concluded that in-situ stress and the mechanical properties of target formation and adjacent formations have a significant influence on the hydraulic fracture containment.

With some limited variations, the P3D model is documented in a number of early literatures [63, 66, 284, 285]. For explanation purpose, we mainly focus on the cell-based P3D model [63, 66], which can be regarded as an extension of the PKN model. The fracture width is still computed in each uncoupled vertical plane, while the fracture is permitted to propagate into adjacent formations and the fracture width is computed by the KGD model or its variations. Taking into account the mass conservation, a 1D flow along the direction of fracture propagation is simulated. A leading edge condition defines the fracture growth velocity. Besides the cell-based P3D model, a lumped model as shown in Fig. 10(b) was also developed by Cleary et al. [62, 66], and grew into FracPro the well-known software tool for hydraulic fracturing design.

The governing equations of the cell-based P3D model were presented by Palmer and Carroll [235, 236] in a more structured manner. A three-layer model with symmetric in-situ stress and toughness is investigated, and the LEFM theory is introduced as the fracture propagation criterion on each vertical plane. The fracture width on each vertical plane is computed based on a plane strain assumption (same as the PKN model). Although the fluid pressure is still assumed to be a constant in each vertical section, the in-situ stress varies with layers, which makes the elasticity Eq. (14) inapplicable. Thus, the elastic equation from the KGD model is used instead:

$$\begin{aligned} w=\frac{8{{h}_{f}}}{\pi {E}'}\int _{{{f}_{L}}}^{1}{\frac{{{f}_{2}}d{{f}_{2}}}{\sqrt{f_{2}^{2}-f_{L}^{2}}}}\int _{0}^{{{f}_{2}}}{\frac{p_{n}({{f}_{1}})d{{f}_{1}}}{\sqrt{f_{2}^{2}-f_{1}^{2}}}} \end{aligned}$$

(44)

where the net pressure $p_{n}$ is the difference between the fluid pressure and the local confining stress, and $h_{f}$ is the fracture half-height. The stress intensity factor $K_{I}$ is computed based on the net pressure:

$$\begin{aligned} {{K}_{I}}=\frac{1}{\sqrt{\pi {{h}_{f}}}}\int _{-{{h}_{f}}}^{{{h}_{f}}}{p_{n}(y)}\sqrt{\frac{{{h}_{f}}+y}{{{h}_{f}}-y}}dy \end{aligned}$$

(45)

The fluid flow is governed by Eqs. (15) and (16) of the PKN model. Carter’s leakoff model is used here.

Rahim and Holditch [250] developed a model (TRIFRAC) which is capable of modelling proppant transport, influence of multi-layers with asymmetric mechanical properties and in-situ stresses. The governing equations are solved by using the finite difference method (FDM). Field data such as well logs are required in this simulator. This model has been applied in many practical cases [251,252,, 252, 253].

Another example of the P3D model is MFrac (Meyer Fracturing simulators), which has been developed since 1986 [204, 205] and is widely used by the petroleum engineering industry. Some other examples and applications of the P3D model can be found in [9, 127, 306]. Comparisons between 2D models (the PKN model and the KGD model) and the P3D model were conducted by Rahim and Holditch [251] and Rahman and Rahman [255]. It is concluded from [251] that the 2D PKN model predicts propped fracture lengths that are closer to those computed with the P3D model, than the 2D KGD model, provided the correct fracture height is input into all models. However, it should be noted that all P3D models ignore the non-local elastic response (the second assumption mentioned at the beginning of this section). The assumption holds for the cases where the fracture length is much larger than the height (>5 times according to [235]), but may result in unacceptable errors when predicting fracture geometry in other cases.

3.5 Planar 3D (PL3D) Model

Along with the development of P3D model, much effort has been made to release the second assumption in the PKN model. This led to the development of the PL3D model, which can be based on either a moving or a fixed mesh system, as shown in Fig. 11.

Fig. 11

The planar 3D (PL3D) model: a a moving mesh system and b a fixed mesh system

Clifton and Abou-Sayed [67] presented the PL3D model based on a moving mesh system and then made further improvements in [68,69,70], which form the basis of the widely used commercial simulator TerraFrac. The governing equations are listed below:

$\circ$:

Elastic equation

The fracture width is related to the 2D distributed fluid pressure with a singular integral equation:

$$\begin{aligned} \begin{aligned} {p}-{{\sigma }_{0}}=&\frac{G}{4\pi (1-\nu )}\int {\int {\frac{\partial }{\partial {y}'}}}\left( \frac{1}{{\mathcal {R}}} \right) \frac{\partial w}{\partial {y}'}\\&+\frac{\partial }{\partial {x}'}\left( \frac{1}{{\mathcal {R}}} \right) \frac{\partial w}{\partial {x}'}d{x}'d{y}' \end{aligned} \end{aligned}$$

(46)

where ${\mathcal {R}}$ is the distance between $\left( x,y\right)$ and $({x}',{y}')$. The above single integral is derived from the elasticity theory for a plane fracture.

$\circ$:

Poiseuille’s law for Non-Newtonian fluid

Instead of simulating a 1D flow as in the P3D model, a 2D non-Newtonian fluid flow is considered, for which Poiseuille’s law Eq. (3) becomes

$$\begin{aligned}&\frac{\partial p}{\partial x}+{{\left[ k\left( 2+\frac{1}{n} \right) \frac{2(n+1)}{n} \right] }^{1/n}}{{\left( \frac{\left| q \right| }{{{w}^{2}}} \right) }^{n-1}}\frac{{{q}_{x}}}{{{w}^{3}}}=0 \end{aligned}$$

(47)

$$\begin{aligned}&\frac{\partial p}{\partial y}+{{\left[ k\left( 2+\frac{1}{n} \right) \frac{2(n+1)}{n} \right] }^{1/n}}{{\left( \frac{\left| q \right| }{{{w}^{2}}} \right) }^{n-1}}\frac{{{q}_{y}}}{{{w}^{3}}}=\rho_{f} {{g}_{y}} \end{aligned}$$

(48)

where $q_{x}$, $q_{y}$ and q are the flow rate along x, y and the resultant flow rate, respectively, k and n are the rheological parameters, $g_{y}$ is the gravity acceleration along the Y direction, and $\rho_{f}$ is the density of fracturing fluid.

$\circ$:

Continuity equation

The continuity equation is similar to the P3D model, but formulated in a 2D space:

$$\begin{aligned} \frac{\partial {{q}_{x}}}{\partial x}+\frac{\partial {{q}_{y}}}{\partial y}+\frac{\partial w}{\partial t}+{{q}_{L}}=0 \end{aligned}$$

(49)

$\circ$:

Fracture propagation criterion

The LEFM theory is used as the fracture propagation criterion along all fracture edges. The critical width is calculated based on the mode I stress intensity factor [67]:

$$\begin{aligned} {{w}_{crit}}=\frac{4{{K}_{I}}(1-v)}{G}{{\left( \frac{a}{2\pi } \right) }^{1/2}} \end{aligned}$$

(50)

where a is a small distance in the order of the mesh size close to the fracture edge. The relative magnitude of the critical width and numerical fracture width close to fracture edge determines whether the fracture advances or not. It is noted that this expression is equivalent to Eq. (21).

In addition, leakoff (simulated by Carter’s leakoff model), thermal effects and proppant transport are also considered by the PL3D model, which can be solved by following a variational approach.

Cleary et al. [65] also contributed to the development of the PL3D model. The PL3D model named 3D HFRAC has a similar framework in terms of governing equations, but the crack propagation is controlled by the so-called leading-edge concept. Rock deformation is solved by a surface integral method and the FEM is used for the fluid flow along fracture. Lam and Cleary [176] improved the model by considering the effect of leakoff using a pressure-related Carter’s leakoff model and verified the model with the analytical results from PKN and KGD models as well as experimental results. A field application is also presented to validate the capacity of their model.

Advani et al. [8] developed a PL3D model to simulate the propagation of planar hydraulic fracture in multi-layered media. Finite element analysis with a migrating mesh representing dynamic fracture domain is conducted to solve the elastic deformation of rock and non-Newtonian fluid flow. The elastic integral equation is adapted to consider varying properties along different layers. Fracture propagation is controlled by the LFEM theory. A time-dependent leakoff is simulated using Carter’s leakoff model.

Ouyang et al. [234] developed a comprehensive PL3D model with proppant transport and leakoff considered. The same elastic equation as [67,68,69] is adopted and solved by FEM. A new form of Poiseuille’s law for non-Newtonian fluid is used without considering the gravity effect. Combining the two equations with the continuity equation leads to a relation between the pressure and width which is solved by FEM. The LEFM is adopted as the hydraulic fracturing criterion and leakoff is simulated by Carter’s leakoff model.

Barree [21] proposed a PL3D model with a fixed mesh, which is the foundation of the popularly used commercial hydraulic fracturing simulator GOHFER$^{\text{\textregistered} }$ (detailed in Sect. 5.6). The tensile strength is used as the fracture propagation criterion. Leakoff is simulated by using a pressure-related expression and proppant transport is not considered. Lee et al. [182] developed a fixed grid finite element algorithm named HYFFIX. Remeshing and solution interpolation between mesh configurations are avoided in the fixed mesh scheme, but the fracture front needs to be explicitly tracked with a separate method. The numerical accuracy is worse at the onset of simulation and gets better with the propagation of hydraulic fracture. Siebrits and Peirce [299] presented a fixed mesh PL3D model based on DDM to simulate planar fracture growth in elastic multi-layer media. Varying properties of material along the vertical direction are considered. A constant pressure is assumed to drive the propagation of fracture. The LFEM theory is used as the fracture propagation criterion. Stress intensity factor is calculated using a nine-node patch of fracture width and is used to update the fracture front. Adachi et al. [3] improved the simulator by adding the modules for fluid flow, leakoff and proppant transport. The FDM is adopted to simulate the fluid flow while the volume of fluid (VOF) method is employed to track the fracture front. A more recent progress is described in [393] which combines the near tip asymptotic solutions into the model to increase the accuracy even on relatively coarse meshes. Different from the PL3D model with a moving mesh, a structured mesh is normally used in the PL3D model with a fixed mesh. Therefore, a suitable mesh size should be chosen to reach a compromise between the accuracy of the model at the beginning of the simulation and the increase of the computational cost with the fracture propagation.

Compared with the 2D model and the P3D model, the PL3D model has a more rigorous framework and fewer assumptions, which in principle allows more accurate predication for hydraulic fracture propagation. On the other hand, a greater computational cost is invoked since the 3D elasticity equation needs to be solved.

3.6 Summary of Classic Fracturing Models

Table 2 summarises the key features of the aforementioned classical hydraulic fracturing models. Warpinski et al. [332] presented a comparative analysis of eleven hydraulic fracturing models, including the 2D, P3D and PL3D models. Base on the test cases with actual field data, the fracture geometry and injection pressure history predicted by these models are discussed.

Table 2 Overview of classic hydraulic fracturing models

An important feature of these classical models is that the rock deformation is evaluated by solving the elastic equation relating the fracture width to fluid pressure directly, instead of discretising the whole domain and solving the deformation based on the constitutive model. By doing so, the complexity of numerical computation and computational cost are significantly reduced. For example, 2D or even 3D fracture geometry is solved in the PKN, KGD and radial model using a 1D mesh, while 3D geometry of hydraulic fracture is solved on a 2D mesh in the PL3D model. The 1D fluid flow is assumed in the PKN and P3D models, and 2D fluid flow for the PL3D models. The solution method can be analytical or numerical. A main limitation of these classical models is that the hydraulic fracture is restricted to propagate along straight line or planar plane. In addition, the effect of natural fractures cannot be easily considered. In order to evaluate hydraulic fracture propagation more realistically and for more complex scenarios, diverse numerical methods have been applied to develop more advanced hydraulic fracturing models, and these are reviewed in the following section.

4 Diverse Numerical Approaches

The effort to predict hydraulic fracture propagation more realistically has been continuing since the beginning of hydraulic fracturing modelling. With the complexity of the models increasing, the analytical analysis commonly used in early-stage models is not sufficient for solving the governing equations associated to the more advanced hydraulic fracturing models, and in order to meet the challenges a diverse range of numerical approaches have been developed by both the petroleum engineering and the fracture mechanics communities.

In the following discussion, we take the discretization method for rock formation as the critical feature to distinguish hydraulic fracturing simulators. The discretization method for formation often has a significant impact on the other elements of the corresponding hydraulic fracturing simulation framework, such as the fluid flow and fracture propagation models, and it normally remains unchanged when the simulation framework is further improved or extended. In addition, when the fluid flow in the reservoir needs to be solved, it is normally solved with a similar numerical scheme as the solid part. When the fluid flow is restricted within the fracture, it typically has a lower dimension than the solid part and hence its solution is relatively easy. Hence, the discussion in this section is organized into three parts: the continuum-based methods, the discontinuum-based methods and the hybrid continuum/discontinuum-based methods. Along with the discussion of specific hydraulic fracturing models, we also highlight their application in various investigation scenarios, such as the mixed-mode propagation of hydraulic fracture, branching, interaction between hydraulic and natural fractures.

4.1 Continuum-Based Methods

4.1.1 Discrete Crack Approaches

• Finite element method (FEM)

As one of the most popular numerical methods in fracture mechanics, FEM has long been adopted to simulate the propagation of hydraulic fracture [7], and the classical FEM hydraulic fracturing models include KGD and radial models, 3D models for planar or non-planar hydraulic fractures, and plane 2D models. Figure 12 provides a schematic illustration for a FEM hydraulic fracturing model.

Fig. 12

A finite element model for hydraulic fracturing [52]

A pioneering work was presented by Boone and Ingraffea [29], who used a KGD-type model to simulate the propagation of hydraulic fracture in poroelastic media. Specifically, FEM is adopted to solve the rock deformation and fluid flow in reservoir, while FDM is used to solve the fluid flow inside fracture following Poiseuille’s law and the continuity equation. The leakoff effect is incorporated into the model by using a pressure-related leakoff model. An equilibrium fracture model based on Dugdale-Barenblatt concept is used to control the fracture propagation, which is analogical to the original KGD model [117]. The numerical results for viscosity-dominated propagation regime (M-vertex solution) in impermeable rocks are verified against the analytical solutions from [308]. Chen et al. [58] developed a cohesive zone finite element-based model for penny-shaped hydraulic fracture. The toughness-dominated hydraulic fracture is investigated numerically and the corresponding solution (K-vertex solution) is verified against the analytical result in [276]. The M-vertex solutions for both KGD-type and penny-shaped hydraulic fractures are presented in the subsequent work [57]. Similarly, Carrier and Granet [43] investigated the 2D propagation of hydraulic fracture in permeable media using the cohesive zone model and compared the numerical solutions of K-vertex, M-vertex, $\tilde{\text {K}}$-vertex and $\tilde{\text {M}}$-vertex with the corresponding analytical solutions. Hunsweck et al. [153] developed a KGD-type hydraulic fracture model which is capable of simulating the transient process from the early-time state to the late-time state. Both the rock deformation and fluid flow are solved using FEM. A significant difference from previous models is that the LEFM theory is used as the fracture propagation criterion. Chen et al. [51] developed a unified FEM-based model to simulate the hydraulic fracturing with and without fluid lag. By transferring between two different boundary conditions for the case with and without fluid lag, the fluid front and fracture tip are tracked accurately and the complex evolution of fluid lag (decrease, increase, vanishment and initiation) is successfully simulated. The commonly observed negative fluid pressure close to the fracture tip is avoided. Yao et al. [361] simulated the propagation of penny-shaped hydraulic fracture in the toughness-storage-dominated regime, the toughness-leakoff-dominated regime and the viscosity-storage-dominated regime by using a cohesive zone finite element-based model.

In PL3D models, the 3D geometry of the hydraulic fracture is computed by solving the coupled equations on a 2D mesh. Another way to model the planar hydraulic fracture propagation is to compute the deformation by solving the equilibrium equation on 3D mesh. Wang et al. [318] investigated the behaviour of planar hydraulic fracture in 3D multi-layered formations using an ABAQUS-based model. Fracture propagation is governed by the cohesive zone model. The effects of in-situ stress, rock elastic modulus and tensile strength on hydraulic fracture height are investigated. In a more general case, Shin and Sharma [294] simulated the propagation of three parallel hydraulic fractures in three-layer formations using ABAQUS. Cohesive zone elements are embedded into the model to simulate the fracture propagation. The drawback is that all hydraulic fractures are limited to be planar.

Secchi and Schrefler [282] developed a full 3D hydraulic fracturing model based on their previous 2D models [280, 283, 302, 303]. Biot’s consolidation is introduced to simulate the rock deformation and fluid flow in reservoir. With the cohesive force considered, the weak form of governing equations for the finite element model are expressed as [301]

$$\begin{aligned}&\int \limits _{\varLambda }{\delta {{\varepsilon }_{ij}}}{{c}_{ijrs}}{{\varepsilon }_{rs}}d\varLambda - \int \limits _{\varLambda }{\delta {{\varepsilon }_{ij}}}\alpha {{\delta }_{ij}}pd\varLambda -\int \limits _{\partial {{\varLambda }_{\tau }}}{\delta {{u}_{i}}}{{\tau }_{i}}d{\partial {\varLambda }_{\tau }} \nonumber \\&\quad -\int \limits _{\varLambda }{\rho \delta {{u}_{i}}}{{g}_{i}}d\varLambda -\int \limits _{\partial \Gamma }{\delta {{u}_{i}}}{{c}_{i}}d\partial \Gamma =0 \end{aligned}$$

(51)

$$\begin{aligned}&\int \limits _{\varLambda }{\delta p\left\{ \left( \frac{\alpha -\phi _r}{{{K}_{s}}}+\frac{\phi _r}{{{K}_{w}}} \right) \frac{\partial p}{\partial t}+\alpha v_{i,i}^{s} \right\} }d\varLambda \nonumber \\&\quad - \int \limits _{\varLambda }{{{\left( \delta p \right) }_{,i}}\left[ \frac{{{k}_{ij}}}{\mu }\left( -{{p}_{,j}}+\rho_{f} {{g}_{j}} \right) \right] d\varLambda }+\int \limits _{\partial \varLambda }{\delta }p{Q}d\partial \varLambda \nonumber \\&\quad +\int \limits _{\partial \Gamma }{\delta }p{{q}_{L}}d\partial \Gamma =0 \end{aligned}$$

(52)

where $\delta {{\varepsilon }_{ij}}$ and ${{\varepsilon }_{rs}}$ are the virtual strain and strain tensor, respectively, $\delta {{u}_{i}}$ is the virtual displacement, ${{c}_{ijrs}}$ is the stiffness tensor, $\alpha$ is the Biot coefficient, ${{\delta }_{ij}}$ is the Kronecker delta, ${{\tau }_{i}}$ is the traction on boundary $\partial {{\varLambda }_{\tau }}$, ${{g}_{i}}$ is the gravity acceleration factor, ${{c}_{i}}$ is the cohesive force on the process zone, $\phi _r$ is the porosity, ${{K}_{s}}$ and ${{K}_{w}}$ are the bulk modulus for rock and fluid, $v_{i}^{s}$ is the velocity vector of the rock formation, ${k}_{ij}$ is the permeability tensor of the porous media, $\mu$ and $\rho_{f}$ are the fluid viscosity and density respectively, Q is the imposed flux on external boundary, and ${{q}_{L}}$ is the leakoff flow rate of fracturing fluid from fracture to the porous media. The integration domains are illustrated in Fig. 12. The fluid flow in fracture is governed by Poiseuille’s law and the continuity equation, and it is coupled with the fluid flow in porous media through leakoff. The corresponding weak form of the governing equation is

$$\begin{aligned} \begin{aligned}&\int \limits _{\Gamma }{\delta p\left\{ \frac{\phi }{{{K}_{w}}}\frac{\partial p}{\partial t}+\frac{\partial w}{\partial t} \right\} }d\Gamma -\int \limits _{\Gamma }{{{\left( \delta p \right) }_{,i}}\left[ \frac{{{w}^{2}}}{12\mu }\left( -{{p}_{,j}}+\rho_{f} {{g}_{j}} \right) \right] d\Gamma } \\&\quad +\int \limits _{\partial \Gamma }{\delta }p{{q}_{L}}d\partial \Gamma =0 \end{aligned} \end{aligned}$$

(53)

The cohesive zone model is adopted and fracture propagates along the element boundary which is closest to the normal direction of the maximum tensile stress. An efficient mesh generator based on Delaunay tessellation is combined into this model to update the mesh with the propagation of hydraulic fracture. Different from the previous finite element based models, this model is capable of simulating mixed-mode propagation of hydraulic fracture in 3D. The propagation of a 3D non-planar fracture at the base of a gravity dam is simulated.

The capacity of FEM-based discrete fracture model in simulating 3D complex hydraulic fracturing is further extended by Salimzadeh et al. [271, 272], Paluszny et al. [238], and Salimzadeh et al. [273]. The Imperial College Geomechanics Toolkit (ICGT) [237] is a three-dimensional finite element simulator for fracture growth and fragmentation of brittle rocks. It models fluid flow and transport through fractured rocks with geomechanically-generated apertures, and simulates thermo-poro-elastic deformation of porous fractured rocks. The deformation of the porous media and the fluid flow inside it are governed by Biot’s poroelasticity theory while the fluid flow inside fracture is governed by the Poisuille’s law and the continuity equation. Both the displacement and pressure field are discretised with FEM [271, 273]. The fracture propagation is predicted according to the stress intensity factors computed by displacement correlation method or energy-based interaction integral. Adaptive remeshing is conducted to update the 3D mesh as the simulation progresses. With this model, simultaneous propagation of multiple 3D hydraulic fractures have been investigated [238, 239, 272].

Effect of natural fractures has also been investigated using the discrete fracture model. Fu et al. [106] developed an explicitly coupled hydro-mechanical model in 2D based on FEM to simulate hydraulic fracturing in discrete fracture networks. FEM and finite volume method (FVM) are used to simulate the rock deformation and fluid flow respectively. The 2D space is discretised by a perturbed structured triangle mesh. LEFM is adopted to determine the propagation of hydraulic fracture. Stress intensity factors are computed using a corrected displacement correlation method. The fracture is assumed to propagate along the element boundary with maximum circumferential stress. A unique module in this model is the so-called joint model utilized to simulate the complex joint behaviours. Chen et al. [55] developed a surrogate-based optimization approach to optimise the hydraulic fracturing treatment based on the numerical model. More recently, they developed a 3D model to simulate the interaction between one main hydraulic fracture and a discrete fracture network consisting of two vertical fracture sets [286]. Wang et al. [326] investigated the interaction between hydraulic fractures and orthogonal bedding planes using FEM with the bedding planes presented by zero-thickness cohesive elements. The debonding zones due to the hydraulic fracture propagation are predicted and can be used to help optimize the perforation cluster spacing.

In the finite element based discrete fracture analysis, fracture surfaces are represented by the mesh so that the fracture width can be readily calculated. But the accompanying remeshing not only increases the computational cost but also results in accuracy problem due to variables mapping between the old and new meshes. Currently, complex propagation of hydraulic fracture in naturally fractured reservoir in 2D and mixed-mode propagation of hydraulic fracture in 3D have been handled. However, when it comes to 3D intersection between hydraulic fracture(s) and natural fractures, the finite element based hydraulic fracturing simulators would encounter with major difficulties on remeshing, computation of stress intensity factors, recognition of fluid flow network, etc.

• Extended/generalized finite element method (XFEM/GFEM)

As a popular numerical method for simulating fracture propagation, XFEM/GFEM has also been applied in simulating hydraulic fracturing [134, 267]. Different from FEM, XFEM/GFEM captures crack deformation via discontinuous fields, namely the partition of unity functions. In the context of elastic problem, the displacement approximation ${u^{h}}$ with the partition of unity is expressed as [217, 260]

$$\begin{aligned} {{u}^{h}}=\sum \limits _{i\in N}{{{u}_{i}}{{N}_{i}}}+\sum \limits _{j\in {{N}^{H}}}{{{b}_{j}}{{N}_{j}}H\text {(}x\text {)}}+\sum \limits _{k\in {{N}^{CT}}}{{{N}_{k}}\left( \sum \limits _{\alpha =1}^{4}{c_{k}^{\alpha }{{\varPhi }_{\alpha }}} \right) } \end{aligned}$$

(54)

where ${u_{i}}$ is the vector of nodal displacement for standard finite elements; $N_{i}$, $N_{j}$ and $N_{k}$ are the standard finite element shape function associated with node i, j and k, respectively; ${b_{j}}$ and $c_{k}^{\alpha }$ are the nodal enriched degrees of freedom associated with the Heaviside function H(x) and near tip asymptotic field function ${{\varPhi }_{\alpha }}$, respectively; N, ${{N}^{H}}$ and ${{N}^{CT}}$ are the set of all nodes, nodes for crack enrichment and tip enrichment, as shown in Fig. 13.

Fig. 13

Node selection for enrichment function

The partition-of-unity method was introduced into hydraulic fracturing simulation by Lecampion [177] and Ren et al. [260]. Specifically, Ren et al. [260] simulated the hydraulic fracturing at the bottom of a gravity dam driven by a uniform constant fluid pressure. Maximum circumferential stress criterion is adopted to determine the fracture propagation direction with stress intensity factors computed by the interaction integral method. Gordeliy and Peirce [123, 124] developed an XFEM simulator with standard governing equations system including elastic equilibrium equation for solid, Poiseuille’s law and continuity equation for fluid, and the fracture propagation governed by LEFM. Both M-vertex and MK-edge solutions are solved numerically in [124] and are compared with the semi-analytical solution in [4]. The fluid lag is tracked in hydraulic fracture parallel to a free surface in [123].

Mohammadnejad and Khoei [216] simulated the 2D propagation of hydraulic fracture along a straight line in porous media using Biot’s theory. Considering the fluid pressure is also discontinuous over the computational domain, the enriched finite element approximation of the fluid pressure is stated as

$$\begin{aligned} {{\varvec{P}}^{h}}=\sum \limits _{i\in N}{{{N}_{i}}}\varvec{{P}}\text { }+\sum \limits _{j\in \left\{ {{N}^{H}},{{N}^{CT}} \right\} }{N_{j}^{enr}\tilde{\varvec{P}}} \end{aligned}$$

(55)

where $\varvec{P}$ and $\tilde{\varvec{P}}$ are the vector of the standard and enriched nodal degrees of freedom, and $N_{j}^{enr}$ is the enriched shape function for node j. Poiseuille’s law is adopted to describe the fluid flow inside fracture while the cohesive zone model is used to represent fracture propagation. The fluid lag is not handled specifically, which results in negative pressure close to the crack tip. Khoei et al. [165] extended this model to model mixed-mode propagation of hydraulic fracture at bottom of the concrete gravity dam by using maximum circumferential stress criterion. Wang [316] simulated mixed-mode propagation of hydraulic fracture initiating from the wellbore under the effect of anisotropic in-situ stress. The behaviour of rock media is considered through Mohr-Coulomb theory of plasticity, while Biot’s theory and Poiseuille’s law are adopted to model the fluid flow in reservoir and inside fracture respectively. Fracture is assumed to propagate to the direction orthogonal to the maximum local tensile stress once the fracture criterion in cohesive crack model is satisfied. Zeng et al. [366] investigated the influence of propagation regimes, fracture length and fracture distance on the stability of the propagation of periodic parallel hydraulic fractures in 2D. Zeng et al. [368] extended this model to an integrated model for simultaneous propagation of multiple hydraulic fractures from a horizontal wellbore. The fluid flow in the whole system including multiple hydraulic fractures, wellbore are simulated with the pressure loss in wellbore and perforation entry both considered. Zeng et al. [369] simulated the mixed-mode propagation of hydraulic fracture in anisotropic poroelastic medium with XFEM, which proves that the anisotropy of the reservoir rock permeability and elastic modulus has a great influence on both the length and orientation of a hydraulic fracture.

Gupta and Duarte [134] simulated 3D non-planar hydraulic fracture propagation using GFEM. A strict assumption is that the fluid pressure remains constant along fracture surfaces. A crack growth criterion based on energy release rate is adopted to determine whether the crack front propagates or not while Schöllmann’s criterion is used for determining the crack propagation direction including kinking angle and twisting angle. Stress intensity factors are extracted using contour integral method. Non-planar propagation of an inclined elliptical hydraulic fracture in multilayer formations with varying in-situ stress is simulated. Gupta and Duarte [135] extended the model to consider the fluid pressure gradient with Poiseuille’s law.

Dahi-Taleghani and Olson [78] investigated the interaction between hydraulic fracture and single natural fracture using an XFEM based model with an energy criterion described in Sect. 2.5. Poiseuille’s law and the continuity equation are adopted to model the fluid flow. This model was extended by Dahi Taleghani and Olson [79] to simulate the propagation of hydraulic fracture in a 2D naturally fractured reservoir. The effect of differential stress, natural fractures orientations and cement bonding on stimulated fracture network are investigated. Dehghan et al. [86] investigated the 3D intersection between hydraulic fracture and a single natural fracture. A sensitivity analysis of various parameters including the strike and dip angles of natural fracture, relative magnitude of the energy release rate for intact rock and natural fracture, etc. is conducted. Recently, the interaction between hydraulic fracture and natural fracture(s) in impermeable and porous rocks are simulated using XFEM by Wang et al. [327] and Xu et al. [349], respectively.

In the framework of XFEM, remeshing is circumvented by introducing the discontinuous fields but the computation of stress intensity factors is not as straightforward as that in FEM. The 3D propagation of nonplanar hydraulic fracture and interaction has been simulated. However, XFEM/GFEM has the same limitation as standard FEM in terms of dealing with complex topology produced from intersection between hydraulic fracture(s) and natural fractures.

• Boundary element method (BEM)

The BEM is another popular modern approach for hydraulic fracturing modelling, and it has been used to simulate both 2D and 3D hydraulic fracture propagations, including the presence of natural fractures. A fundamental difference between the BEM and standard FEM is that the discretization is implemented only on the boundary in BEM but over the whole domain in FEM. This reduces the difficulty in terms of mesh update and computational cost when simulating dynamic propagation of hydraulic fracture. In addition, the BEM also has some advantages in specific problems with infinite (or semi-infinite) domain or discontinuous solution spaces [139].

Dong and de Pater [93] developed a simple 2D hydraulic fracturing model using displacement discontinuity method (DDM), an indirect BEM formulation. As a kind of BEM formulation designed for problems with crack-like geometries, DDM is the most commonly used formulation of BEM in this area. The discretised form of displacement discontinuity equation is expressed as

$$\begin{aligned} {{\sigma }_{Ni}}= & {} \sum \limits _{j=1}^{N}{{{A}_{NSij}}{{D}_{Sj}}}+\sum \limits _{j=1}^{N}{{{A}_{NNij}}{{D}_{Nj}}} \end{aligned}$$

(56)

$$\begin{aligned} {{\sigma }_{Si}}= & {} \sum \limits _{j=1}^{N}{{{A}_{SSij}}{{D}_{Sj}}}+\sum \limits _{j=1}^{N}{{{A}_{SNij}}{{D}_{Nj}}} \end{aligned}$$

(57)

where ${{\sigma }_{Ni}}$ and ${{\sigma }_{Si}}$ are the normal and shear stress boundary condition on node i, respectively; A is the influence coefficient matrix, e.g. ${{A}_{NSij}}$ reflects the influence of the shear displacement discontinuity at node j on the normal stress at node i; D is the displacement discontinuity, e.g. ${D}_{Sj}$ is the shear displacement discontinuity at the node j; and N is the total element number. The coupled problem is simplified by assuming a constant and uniform fluid pressure. Maximum circumferential stress criterion is utilized to determine the fracture propagation direction with stress intensity factors computed by displacement extrapolation method. The mixed-mode propagation of hydraulic fracture and interaction between multiple hydraulic fractures are simulated.

Zhang et al. [379] presented a more rigorous model based on DDM with fluid flow governed by Poiseuille’s law and the continuity equation. Both slip and fluids fronts are tracked in addition to the propagation of crack tip. Interaction between multiple hydraulic fractures initiating from a wellbore is simulated. Wu and Olson [341] simulated simultaneous propagation of multiple hydraulic fractures along a horizontal wellbore with fluid flow in both hydraulic fractures and horizontal wellbore considered. Zhang and Jeffrey [373] and Zhang et al. [377, 378] developed a DDM-based 2D model to simulate impact of natural fractures. The fluid flow is governed by Poiseuille’s law and the continuity equation, which are solved by using the FDM. Fractional stress along natural fracture surfaces is governed by Coulomb’s frictional law without cohesion. Closed natural fractures are assigned with a minimum fluid conductivity. Both the slip and fluid fronts are solved. Maximum circumferential stress criterion is adopted to determine the fracture propagation direction when new fracture surfaces are generated. In numerical cases, single natural fracture perpendicular to hydraulic fracture and simple natural fracture network are studied. Offset of hydraulic fracture from an orthogonal natural fracture is simulated by introducing a secondary flaw on the natural fracture artificially.

Olson [229] and Olson and Taleghani [230] investigated simultaneous propagation of multiple hydraulic fracture from a horizontal wellbore in a 2D naturally fractured reservoir using DDM. Fluid pressure is assumed to be uniform and constant and is applied on the surfaces of hydraulic fractures and natural fractures connected to them. A set of natural fractures with specific length and orientation are considered. A friction coefficient of 0.6 and zero-cohesion are applied on the natural fractures. Fracture propagation direction for newly generated fracture surfaces is determined by maximum circumferential stress criterion. The numerical cases demonstrate that the final fracture network is determined jointly by natural fracture networks, in-situ stress and fluid injection pressure. More recently, Wu and Olson [342] improved the model by introducing the fluid flow simulation into the system. A set of natural fractures with specific orientation but with random length is considered and a crossing criterion is used to determine whether the hydraulic fracture would cross the natural fracture or penetrate into it. A sensitivity analysis of perforation-cluster spacing, in-situ stress and natural fracture patterns is conducted.

Xie et al. [348] developed a DDM-based 2D model named FEACOD to simulate propagation of hydraulic fracture in naturally fractured reservoir. An explicit approach is used which contains four steps: (1) to compute fluid flow and flow leakage using Poiseuille’s law and Darcy’s law; (2) to update the fluid pressure for the compressible fluid; (3) to compute the new fracture deformation using DDM; and (4) to update the fluid pressure for the compressible fluid. Both the fracture initiation and propagation are simulated in this model. Tensile fracture is initiated once the tensile strength is larger than the rock tensile strength while shear fracture is initiated when Mohr-coulomb failure criterion is satisfied. Fracture propagation is governed by the F-criterion based on LEFM. A set of natural fractures with random length are considered in numerical cases. More recently, Xie et al. [347] verified this model with KGD model solution and simulated interaction between hydraulic fracture and a single natural fracture. Similar 2D models are also presented in other literatures, e.g. [384].

DDM has also been applied in extending the P3D and PL3D models reviewed in Sects. 3.4 and 3.5 to simulate the simultaneous propagation of multiple hydraulic fractures in 3D space with the stress shadowing effect considered, which is the concept of Unconventional Fracture Model (UFM) [173]. Kresse et al. [174] simulated the interaction between multiple hydraulic fractures with P3D model. The stress shadowing effect is estimated with a 2D DDM model, and the hydraulic fractures are also permitted to curve on the plane defined by the 2D DDM model but kept vertical. Kresse and Weng [172] further improved the model to adopt a simplified 3D DDM to estimate the 3D stress shadowing effect. Chen et al. [56] investigated the simultaneous growth of hydraulic fractures in multiple horizontal wells with a fixed mesh PL3D model. The stress shadowing effect between the multiple planar hydraulic fractures are accurately simulated with a full 3D DDM and the FVM is used to solve the fluid flow inside hydraulic fractures. The fracture tip is determined by the tip asymptotic solution and is tracked with the level set method.

Several BEM-based full 3D models have also been developed [44, 269, 310, 313, 354]. For example, based on the general purpose 3D fracture analysis code (FRANC3D), the software tool HYFRANC3D [44] is developed to simulate multiple, arbitrary, nonplanar 3D fractures. Maximum circumferential tensile stress criterion, maximum energy density and minimum strain energy density are implemented to determine the fracture propagation direction. Fluid flow inside fracture is governed by the continuity equation and Poiseuille’s law, and solved using FEM. Leakoff is modelled by Carter’s leakoff law and poroelastic effect is not considered. HYFRANC3D has been applied to investigate nonplanar propagation of single hydraulic fracture and the interaction between closely spaced but disjoint hydraulic fractures [94, 147, 257]. The other BEM-based full 3D models share most of the important features with this model, which includes maximum circumferential tensile stress criterion for fracture propagation, Poiseuille’s law and the continuity equation for fluid flow, and Carter’s leakoff model for leakoff effect. But the models developed by Vandamme and Curran [313] and Yamamoto et al. [352,353,, 353, 354] are both based on DDM, while the one developed by Rungamornrat et al. [269] and Castonguay et al. [46] is based on symmetric Galerkin boundary element method (SGBEM). Vandamme and Curran [313] simulated simultaneous propagation of two parallel closely spaced penny-shaped hydraulic fractures. Yamamoto et al. [354] investigated the interaction between multiple hydraulic fractures initiated from a single wellbore or different wellbore cases. Rungamornrat et al. [269] simulated propagation of a single hydraulic fracture initiating from an inclined wellbore under the effect of in-situ stress varying with layers and Castonguay et al. [46] simulated simultaneous propagation of multiple disjoint hydraulic fractures from horizontal or vertical wellbore.

More recently, Kumar and Ghassemi [175] developed a poroelastic 3D DDM-based hydraulic fracturing model to simulate the simultaneous propagation of multiple hydraulic fractures. Xie et al. [346] applied 3D DDM in simulating the penetration of hydraulic fracture into the bedding planes. Dontsov and Suarez-Rivera [96] investigated the different propagation regimes of multiple hydraulic fractures in 3D space using the numerical simulator FrackOptima.

Compared with other continuum approaches such as FEM and XFEM, BEM is easier to implement with lower computational cost. Another advantage is that the mechanical behaviour of natural fractures such as friction between opposite fracture surfaces are easy to be modelled in DDM formulation. However, the intersection of arbitrary 3D hydraulic fractures remains an unsolved problem in the scheme of BEM, and advanced constitutive models such as elastoplasticity are not permitted in this scheme.

• Peridynamics

Silling [300] proposed the peridynamics theory to represent a material as a composition of material points, each of which interacts with the other material points inside a horizon, as shown in Fig. 14. The interaction between the material points is related to the deformation and constitutive properties of the material.

Fig. 14

Interation of a material point with its neighbouring points

Compared with classical continuum mechanics, the peridynamics theory has its own advantages. It uses spatial integral instead of partial differential equations for motion equations, which then avoids the singularity problem and combines continuous and discontinuous descriptions together. The peridynamic equation of motion at a reference position of $\varvec{x}$ and time t is given as [231]:

$$\begin{aligned} \rho (\varvec{x})\ddot{\varvec{u}}(\varvec{x},t)=\int _{H_{x}}{\varvec{f}(\varvec{x'}-\varvec{x},\varvec{u'}-\varvec{u})dV}+\varvec{b}(\varvec{x},t) \end{aligned}$$

(58)

where $\rho$ is the mass density, $\varvec{u}$ is the displacement vector field, $H_{x}$ is a horizon with a size (i.e., radius) of $\delta$, $\varvec{f}$ is the force vector per unit volume squared between two material points, dV is the differential volume, $\varvec{b}$ is a prescribed body-force density field. Another advantage of the peridynamics theory is that no extra criterion is need for crack initiation and propagation as the crack growth can occur spontaneously with only one bond-break (interactions) criterion. The bond between the material points is assumed to break once the elongation of a bond (determined by the geometry, loading conditions and loading history) is greater than a certain critical value $S_{0}$ defined as [199]:

$$\begin{aligned} S_{0}={\left\{ \begin{array}{ll} \sqrt{\frac{4\pi G_{c}}{9E\delta }}, \text { Plane stress} \\ \sqrt{\frac{5\pi G_{c}}{12E\delta }}, \text { Plane strain} \\ \sqrt{\frac{5G_{c}}{6E\delta }}, \text { 3D} \end{array}\right. } \end{aligned}$$

(59)

A macroscopic fracture initiates when the discontinuous space forms due to a series of bond-break.

The peridynamics theory has been applied in hydraulic fracturing simulation recently, due to its strength in modelling crack problems. By using the analogy between poroelasticity and thermoelasticity, Oterkus et al. [231] presented a new fully coupled poroelastic peridynamic formulation. The fluid flow equation in porous media in peridynamic form can be written as

$$\begin{aligned} \frac{1}{M}{\dot{P}}(\varvec{x},t)=\int _{H_{x}}\left( {k_r}\frac{{P}(\varvec{x'},t)-{P}(\varvec{x},t)}{\left| \varvec{x'}-\varvec{x}\right| }-\frac{c}{2}\alpha \gamma _p{\dot{e}}\right) d{V}+\frac{Q}{\rho_{f} } \end{aligned}$$

(60)

where M is the Biot modulus, $\alpha$ is the Biot coefficient, P represents the pore pressure, $k_{r}$ is the rock permeability, $\gamma _p$ is the coefficient of pore pressure, c the bond constant, ${\dot{e}}$ is the time rate of change of extension, Q is the fluid source, and $\rho_{f}$ is the fluid density. Combined with the above peridynamic motion equation, a fully coupled equation system is presented. The system can be solved explicitly by a staggered method with fixed time stepping. The displacement field is solved with motion equation while the pore pressure field is solved with fluid flow equation in porous media. This formulation is verified by two benchmark consolidation problems and a fluid-driven fracture propagation case.

Ouchi et al. [232] developed the state-based peridynamic formulations with the presence of both porous media flow and fracture flow. Combined with the existing peridynamic solid formulation, a model is developed to simulate fluid-driven fractures in an arbitrary heterogeneous poroelastic medium. After verifying this model with the well-known KGD model, Ouchi et al. [233] used his model to simulate hydraulic fractures in more complex natural fracture networks and investigated the key parameters influencing the interactions between the hydraulic and natural fractures. Nadimi et al. [222] presented a novel 3D simulation of the hydraulic fracturing initiation and propagation in a heterogeneous geological formation by using a linear-viscoelastic peridynamics model. The interaction between induced fractures and a pre-existing fracture is investigated, as well as the influence of the angle of approach and differential horizontal stress on the fracture propagation behaviour.

As a non-local continuum mechanics approach, peridynamics proves its ability when solving hydraulic fracturing. It is mesh free, which makes it easier to model complex fracture networks. Also, with a relatively easy crack propagation criterion, the fracture initiation and propagation can be captured spontaneously without complicated computations.

4.1.2 Smeared Crack Approaches

For the discrete fracture analysis approaches reviewed in Sect. 4.1.1, a mesh is used for the discretization of rock formations and it normally needs to be updated constantly to present the fracture surface as it propagates, especially for the mixed-mode fracture. This problem is circumvented in the smeared fracture analysis, where both the fracture and surrounding media are represented by the elements but in different states.

• Damage-based smeared crack models

• Finite element method (FEM)

Ji et al. [157] developed a hydraulic fracturing model coupled with geomechanical simulation, reservoir flow and fracture modelling. Rock deformation and fluid flow in fracture and reservoir are computed in the first two modules by using FEM and FDM respectively on identical 3D mesh. The element type shifts to the so-called freed element once the effective minimum stress is below the rock tensile strength. The permeability of freed element is computed according to rock permeability and the fracture permeability is computed according to Poiseuille’s law. Poroelastic effect is presented in this model. This model can simulate the fracture initiation and propagation, post-frac clean-up and well performance in a unified mode.

Fig. 15

RFPA3D structure: a finite element discretization of computational domain; and b computation of virtual fracture width, where the four sub-figures are (in the order of arrows): element before deformation, element after deformation, virtual fractures and fluid channels

Li et al. [188] simulated the propagation of 3D hydraulic fracture using three-dimensional Rock Failure Process Analysis-Parallel model (RFPA3D). This model follows the same assumptions and framework RFPA 2D [323, 358], and Fig. 15 provides a schematic illustration of the simulator. Biot’s consolidation theory is used to solve the rock deformation and fluid flow over the whole computational domain. The permeability for each element is computed based on the element deformation. As shown in Fig. 15b, three virtual orthogonal fractures with the same width d are constructed inside the element after deformation. The permeability of the element along each direction is computed based on Poiseuille’s law using Eq. (5). The fracture width w is estimated by $w\approx {{\varepsilon }_{v}}\root 3 \of {V}/{3}$, with V denoting the original volume of the element. Tensile and shear failure are considered by using the maximum tensile stress (or strain) criterion and Mohr-Coulomb failure criterion, respectively. An elastic-brittle damage constitutive model with a specific residual strength is used. The elastic modulus remains unchanged in the elastic stage and degrades gradually as the damage progresses according to

$$\begin{aligned} E_{e}=(1-\beta )E \end{aligned}$$

(61)

where E is the elastic modulus of the undamaged material and $\beta \in (0,1)$ is the damage variable computed according to the element stress state. Weibull distribution is adopted to describe the heterogeneity of rock properties such as Young’s modulus and the strength properties. These features allow the model cope with complex evolution of hydraulic fractures in heterogeneous rock media. More recently, the RFPA3D has developed into a software code named RFPA-Petro and has been applied in field-scale simulation of multiple hydraulic fractures propagation to guide the hydraulic fracturing design [191].

Wangen [329] developed a 3D hydraulic fracturing model based on their previous 2D model [328]. Biot’s consolidation theory is used to couple the rock deformation and pore pressure, but the seepage equation (12) only covers the undamaged rock. The governing equation for fluid flow inside fracture is constructed by combining the continuity equation and Poiseuille’s law:

$$\begin{aligned} {{\phi }_{F}}{{c}_{\text {f}}}\frac{\partial p}{\partial t}-\nabla \left( \frac{{{k}_{F}}}{\mu }\nabla p \right) =-\frac{\partial {{\phi }_{F}}}{\partial t} \end{aligned}$$

(62)

where ${{\phi }_{F}}=\phi _{r} +{\varDelta V}/{V}$ is the fracture porosity with $\phi _{r}$ denoting the porosity of rock and $\varDelta V$ the variation of element volume after deformation, ${{c}_{\text {f}}}$ is the fluid compressibility, ${{k}_{F}}$ is the permeability of fractured element calculated as the arithmetic mean of the rock permeability $k_{r}$ and the fracture permeability ${{k}_{f}}={{w}^{2}}/12$. The maximum opening along the three spatial directions is taken as the fracture width w. The Eqs. (11), (12) and (62) are all solved using a FEM scheme on a uniform 3D mesh. An element is assumed to be fractured once the propagation criterion $\max ({{\varepsilon }_{xx}},{{\varepsilon }_{yy}},{{\varepsilon }_{zz}})>{{\varepsilon }_{frac}}$ is satisfied, where ${{\varepsilon }_{frac}}$ is the presumed strain threshold. It is noted that the fracture propagation criterion is only capable of modelling tensile failure. Propagation of hydraulic fracture in 3D homogeneous and heterogeneous rocks is simulated in numerical cases. This model was further developed to simulate field-scale hydraulic fracturing in anisotropic stress field [330].

The interaction of hydraulic fracture and single natural fracture was investigated in a poroelastic model by Rahman and Rahman [256]. The wellbore, reservoir, hydraulic fracture and natural fracture are represented by different types of elements with different properties in the finite element formulation. Biot’s consolidation theory is adopted to solve the rock deformation and pore pressure in the computational domain and uniform pressure is applied inside the fracture and at wellbore. Dilation of the natural fracture is evaluated directly according to the deformation of elements and crossing or re-initiation of hydraulic fracture are checked by tensile failure criterion.

Different from the discrete fracture models, fracture surfaces are not represented explicitly by the mesh in the smeared fracture models. This brings two benefits: (1) it is not compulsory to update the mesh with fracture propagating; and (2) advanced constitutive models are relatively easy to be implemented. Smeared fracture models normally use the maximum tensile stress (strain) criterion and Mohr-coulomb criterion to determine fracture propagation while discrete fracture models normally use the fracturing criteria based on the LEFM theory or cohesive zone model.

• Finite difference method (FDM)

Zhou and Hou [391] simulated the propagation of planar 3D hydraulic fracture with a 3D model in the framework of FLAC3D. Rock deformation is computed by the mechanical option in FLAC3D and fracture width is represented by the plastic displacement. Fluid flow inside fracture governed by Poiseuille’s law and the continuity equation are modelled using a dedicated flow simulator added into FLAC3D, while reservoir flow governed by Darcy’s law is simulated by FLAC3D. Leakoff is computed according to Darcy’s law. Fracture front elements transforms into completely fractured element when the tensile failure criterion is satisfied. Three kinds of elements in the model are shown in Fig. 16. By using the smeared crack model, the propagation of planar hydraulic fracture in multilayer formations is simulated.

Fig. 16

Fracture representation with three types of elements: fractured element, fracture front element and non-fractured element

This model was further improved by Zhou et al. [392] and was used to investigate the cause for low-efficient stimulation. Proppant transport, fracture closure and contact are all simulated. It is concluded that full closure of the fracture at the perforation results in low productivity. Compared with the full 3D models, the capacity of the FLAC3D-based model is still limited.

More recently, Ren et al. [261] investigated the 3D propagation path of a two-cluster hydraulic fracture system in horizontal wells. The numerical elements are also divided into three types: intact rock element, fracture element and tip element. The deformation of the intact rock element and tip element are governed by linear elastic theory while the deformation for fracture element is consisted of both the deformation of the intact rock and fracture sets according to the embedded element method. The fluid flow governed by Poisuille’s law and the continuity equation is solved with the finite volume method. The tip elements turn into the fracture element once the tensile failure criterion is satisfied. The effect of the in-situ stress anisotropy, Young’s modulus heterogeneity, well deviation on the propagation of hydraulic fractures are systematically investigated and the mixed-propagation of hydraulic fractures are presented.

• Phase field model (PFM)

As a mathematically rigorous framework to solve interface problems, PFM has been applied in many areas including solidification dynamics, coarsening and grain growth, multiphase flow, microstructure evolution, fracture mechanics. Some of these problems have diffuse interfaces while the others have sharp ones. In the latter case, the sharp interface is replaced by a diffuse interface represented by a temporal auxiliary field. Indeed, this kind of diffuse-interface theory had been investigated long before the term of PFM was coined in [103], and some best known studies include Cahn-Hilliard equation [39] and Allen-Cahn equation [38]. Application of PFM in fracture mechanics can be tracked back to the work by Francfort and Marigo [105] and Bourdin et al. [31] and related works have been reviewed by Ambati et al. [12]. Different from the discrete crack approaches and damage-based smeared crack models where the fracture propagation is judged according to the strain and stress states of the material in the vicinity of a crack tip, PFM treats the fracture propagation together with the deformation of surrounding medium as an energy minimization problem according to the minimum total potential energy principle [52, 130]. An additional degree of freedom called phase field is introduced to present the evolution of fracture and incorporate the fracture surface energy into the total energy, as shown in Fig. 17. For a very small parameter $\eta$, the diffusive crack represented by the phase field will approximate to the sharp crack in discrete crack approaches. In essence, it can be regarded as an energy-based analysis with a mathematical approximation instead of a damage-based model.

Fig. 17

A solid body $\varLambda$ with an internal discontinuity approximated by the phase field $\varphi (\varvec{x},t)$ with controlling parameter $\eta$ [52]

PFM has also been applied in hydraulic fracturing modelling with significant progress in recent years. Bourdin et al. [33] developed a phase-field hydraulic fracturing model by extending their previous work on traditional fracture problem [31, 32, 105] to include the influence of uniform fluid pressure along fracture surface. The bulk energy functional defined over a 2D or 3D domain $\varLambda$ is expressed as:

$$\begin{aligned} \begin{aligned} E(\varvec{u},\varphi )=&\int \limits _{\varLambda }\frac{1}{2}\varphi ^{2}\varvec{\varepsilon }:{\varvec{C}}:\varvec{\varepsilon }d{\varLambda }-\int _{\partial {{\varLambda }_{\varvec{\tau } }}}{\varvec{\tau } \cdot \varvec{u}d\varLambda }-\int _{\varLambda }{\varvec{f}\cdot \varvec{u}d\varLambda } \\&-W_{fluid}+{{G}_{c}}{{\mathcal {H}}^{N-1}}\text {(}\Gamma \text {)} \end{aligned} \end{aligned}$$

(63)

where $\varvec{u}$ and $\varvec{\varepsilon }$ are the displacement and strain, respectively, $\varvec{\tau }$ is the external force applied on the boundary $\partial {{\varLambda }_{\tau }}$, $\varvec{f}$ is body force, and ${{H}^{N-1}}\text {(}\Gamma \text {)}$ is the N-1-dimensional Hausdorff measure of $\Gamma$ and is expressed as

$$\begin{aligned} {{\mathcal {H}}^{N-1}}=\frac{1}{2}\int _{\varLambda }{\frac{{{(1-\varphi )}^{2}}}{\eta }+\eta {{\left| \nabla \varphi \right| }^{2}}d\varLambda } \end{aligned}$$

(64)

where $\varphi$ is the phase field and $\eta$ is a small parameter. The work done by the fluid pressure inside the fracture is expressed as:

$$\begin{aligned} {{W}_{fluid}}=\int \limits _{\Gamma }{p(\mathbf{u ^{+}}-\mathbf{u ^{-}})\cdot \mathbf{n} ds}\approx \int \limits _{\varLambda }{p\mathbf{u} \cdot \nabla \varphi d\varLambda } \end{aligned}$$

(65)

The displacement $\varvec{u}$ and phase field $\varphi$ are computed according to the minimization of the total free energy E of the system. The variational principle of the physical problem can be expressed as:

$$\begin{aligned} {[}\varvec{u},\varphi ]=Arg\left\{ \text {inf} E(\varvec{u},\varphi ) \right\} \end{aligned}$$

(66)

The weak form of the governing equations are obtained by imposing $\delta E=0$ for arbitrary $\delta u$ and $\delta \varphi$ (derivation details can be found in [218]) and are solved using the standard FEM with a monolithic or staggered scheme.

This model was extended to include the poroelastic effect according to Biot’s poroelasticity theory in [362]. Taking into account the pore pressure effect, the bulk energy functional (63) becomes

$$\begin{aligned} \begin{aligned} E(\varvec{u},\varphi )=&\frac{1}{2}\int _{\varLambda }{\varvec{C}\left( \varphi \varvec{\varepsilon } -\frac{\alpha }{3K_{s}}{p}\varvec{I} \right) :\left( \varphi \varvec{\varepsilon } -\frac{\alpha }{3K_{s}}{p}\varvec{I} \right) d\varLambda }\\&- \int _{\partial \varLambda }{\varvec{\tau } \cdot \varvec{u}ds}-\int _{\varLambda }{\varvec{f}\cdot \varvec{u}d\varLambda }-\int _{\varLambda }{{p}\varvec{u}\cdot \nabla \varphi d\varLambda }\\&+{{G}_{c}}{{H}^{N-1}}\text {(}\Gamma \text {)} \end{aligned} \end{aligned}$$

(67)

where $\alpha$ is the Biot coefficient and $K_{s}$ is the bulk modulus. In this equation, the equivalent work done by the fluid can be expressed as:

$$\begin{aligned} {W_{fluid}}=\int \limits _{\varLambda }{{{\varphi }^{2}}\alpha p\nabla \cdot \varvec{u}d{\varLambda }}+\int \limits _{\varLambda }{p\varvec{u}\cdot \nabla \varphi d\varLambda } \end{aligned}$$

(68)

For the bulk energy expressions in Eqs. (63) and (67), a compressive fracture with negative fracture volume is also admissible. In order to avoid such unreasonable results, a new form of strain energy density based on the so-called unilateral contact condition proposed by Amor et al. [13] is used in this model. An alternative form of the strain energy to solve this problem is described in [208] and are discussed together with Amor’s form by Borden et al. [30]. Fluid flow in fracture and reservoir are simulated in a unified framework and are governed by the continuity equation and generalized Darcy’s law [362]:

$$\begin{aligned} \frac{\partial }{\partial t}\left( \phi _{r} \rho_{f} \right) =-\nabla \cdot \left( \rho_{f} \mathbf{U} \right) +Q \end{aligned}$$

(69)

where $\phi _{r}$ is the porosity of the porous medium, $\rho_{f}$ is the fluid density, Q is the source term, and $\mathbf{U}$ is the fluid velocity expressed as

$$\begin{aligned} \mathbf{U} =-\frac{{{k}_{mult}}{} \mathbf{K} }{\mu }\cdot \left( \nabla p+\rho_{f} \varvec{g}\nabla Z \right) \end{aligned}$$

(70)

where $\mathbf{K}$ is the permeability tensor, Z is the elevation, the coefficient ${{k}_{mult}}$ equals to ${{k}_{f}}/{{k}_{r}}$ if $\varphi$ is lower than a threshold and equals to 1 otherwise, ${{k}_{f}}$ is the fracture permeability, and ${{k}_{r}}$ is the rock permeability. The two equations derived from minimizing bulk free energy and the fluid equation are solved in a staggered way. More specifically, displacement field is solved firstly by minimizing the bulk energy functional with given pressure and phase field and then phase field is solved in the same procedure but with given pressure and phase field in each iteration. FEM is employed in both steps. Finally, fluid pressure is updated by solving the fluid flow equation with a reservoir simulator. It is noted that the numerical approach and solution scheme (staggered or monolithic) may vary.

Based on this model, Yoshioka and Bourdin [362] investigated the effect of natural fracture(s) on hydraulic fracture propagation with natural fracture(s) represented by zero phase field value. Offset of hydraulic fracture when passing a natural fracture in 2D and complex interaction between hydraulic fracture and four natural fractures with different dip angles in 3D space are simulated.

Mikelic et al. [212, 213] and Wheeler et al. [337] also applied PFM to model hydraulic fracturing. Several new contributions are made in [212]: (1) poroelastic effect is considered and fluid pressure field is solved together with the displacement and phase field; (2) media heterogeneity is considered; and (3) 3D propagation of a penny-shaped hydraulic fracture is simulated. Wick et al. [338] simulated the interaction between hydraulic fractures in 2D and 3D poroelastic media. The intersection between hydraulic fracture and natural fracture(s) in 2D is also simulated by Mikelić et al. [214, 215]. In order to increase the simulation scale, adaptive mesh is implemented by Lee et al. [180]. Propagation of two perpendicular hydraulic fractures in homogeneous and heterogeneous media is simulated. Fracture permeability is computed according to Poiseuille’s law and an interpolated permeability is used in the transition zone.

Miehe et al. [211] simulated 3D propagation of hydraulic fracture in a porous block with four existing fractures by extending their previous work about PFM for traditional fracture problems [143, 144, 208, 209]. Simultaneous propagation of multiple hydraulic fractures starting from different locations on a 3D borehole is represented in [207]. Some of these hydraulic fractures intersect with each other to form a complex 3D fracture network. A validation of the PFM for hydraulic fracturing with experimental results was presented in [142].

Although PFM is a mature and well-validated model for traditional fragmentation problems, the implementation of fluid effect in existing PFM for hydraulic fracturing is non-uniform in literatures [207, 337, 362]. Chen et al. [52] compared the three different ways for combining fluid effect into the phase field framework and proposed a more accuracy model. The new model is solved with a hybrid FEM-FVM solver and is applied in solving the propagation of hydraulic fracture in a naturally fractured reservoir.

While PFM simulation of hydraulic fracturing is still under rapid development [186, 363], the existing studies have demonstrated that PFM is a powerful method to deal with complex propagation of hydraulic fracture(s) even in naturally fractured reservoir. The PFM approach has several advantages: (1) there is no need to represent the discrete fracture surfaces by remeshing, which makes it possible to simulate the complex intersection of hydraulic and natural fractures especially in 3D space; (2) no extra fracture propagation criterion is needed since Griffith’s criterion has been recast into the bulk energy functional, which circumvents the computation of stress intensity factors in complicated conditions; and (3) media heterogeneity is easy to be introduced into the solution scheme. But it should be noted that these advantages do not come without a cost, at least for the current PFM models. The computational cost of PFM simulation is high, especially when a relatively sharp interface is to be captured. Very fine mesh and small time step are essential for validation with semi-analytical analytical solutions in Sect. 3.2.

4.2 Discontinuum-Based Methods

• Discrete element method (DEM)

Cundall [76] developed the first DEM model to analyse rock mechanics problems. Different from the continuum approach, this model describes the rock media as a discrete system of deformable polygonal blocks. Newton’s second law for blocks and force-displacement law for contacts between blocks are applied alternatively in the solution procedure. Based on this pioneering work, ITASCA Consulting Group developed a 2D numerical software named Universal Distinct Element Code (UDEC) and then its 3D version named Three-Dimensional Distinct Element Code (3DEC). By using rigid disks or spherical particles, DEM is implemented in a simplified way, which contributes to the development of Particle Flow Code in 2D and 3D (PFC2D and PFC3D). These DEM tools, i.e. UDEC, 3DEC and PFC2D, have all been used to simulate hydraulic fracturing. To support coupled hydro-mechanical analysis, fluid flow along the edges has been integrated into UDEC since 1985 [77] and is described using Darcy’s law for contact and Poiseuille’s law for joint, as shown in Fig. 18. In the current framework of UDEC, each block can be either rigid or deformable. Macro deformation and fracture propagation (change of joint aperture in the context of UDEC) can be readily represented by using dedicated constitutive models for blocks and joints.

Fig. 18

Sketch of UDEC model with fluid flow: (a) flow system consisting of voids and fluid channel (contacts or joints) and (b) constitutive behaviour of contacts in shear and tension [193]

As one of the earliest works in this area, Harper and Last [138] investigated the aperture change of two mutually orthogonal sets of parallel fractures during hydraulic fracturing using UDEC, and studied the effects of in-situ stress and pore pressure. Under different block patterns and in-situ stress regimes, Zhang et al. [374] investigated hydraulic fracture propagation near wellbore. Later, the influence of other factors including rock properties, injection flow rate and fluid viscosity were also studied [224, 371]. Zangeneh et al. [365] simulated the interaction between hydraulic fracture and natural fractures by embedding natural fractures into the network of incipient joint and assigning zero cohesion and zero tensile strengths for the natural fractures. The numerical results show that the hydraulic fracture tends to cross the natural fractures under high differential stresses and large approach angles.

Using 3DEC, Hamidi and Mortazavi [137] simulated 3D hydraulic fracture propagation in intact rocks. A so-called fictitious joint technique is used to simulate the initiation of hydraulic fractures. A sensitivity study of in-situ stress, rock properties and operational parameters is conducted, which shows hydraulic fracturing is affected more by in-situ stresses than rock properties. Nagel et al. [223] simulated hydraulic fracture propagation in a naturally fractured reservoir with 350 natural fractures using 3DEC. The numerical simulation demonstrates microseismic events not only occur in areas reached by hydraulic fractures but also happen due to the shear failure of dry natural fractures. Thus simply assuming the range of microseismic events to be equal to the stimulated reservoir volume will lead to an over-estimate of hydraulic fracturing effect, especially in the case of high viscosity. Damjanac and Cundall [81] used 3DEC for simulating hydraulic fractures in a reservoir with fully (or sparsely) connected natural fracture network, and a better stimulation is observed for the reservoir with fully connected natural fracture network.

PFC has also been used in hydraulic fracturing simulation but restricted in 2D models. PFC differs from UDEC and 3DEC in several aspects: (1) the discrete elements (disk in 2D and sphere in 3D) are rigid while the blocks in UDEC or 3DEC can be either deformable or rigid; (2) interaction between discrete elements is easier to be modelled in PFC compared with UDEC and 3DEC, which makes the PFC more efficient; and (3) the extent of displacement is not limited in PFC [325]. More specifically, fractures are represented by voids and channels in PFC, and the interaction between particles can be described by several built-in contact models, which are capable of simulating the shear and/or tensile forces between particles. Fluid flow is simulated using a void-channel system, where the fluid flow through the channel is normally governed by the Poiseuille’s law and the fluid pressure change inside voids is computed according to the continuity equation and fluid compressibility property [10, 325, 389].

Based on PFC2D and with extra developments, Al-Busaidi et al. [10] computed the acoustic emissions in the hydraulic fracturing model and compared them with records from laboratory experiments. By analysing these data, they conclude that the hydraulically deduced fracture in granite sample is in tensile mode and the shear cracks emerged in the experiment are due to the natural fracture slip. After that, they investigated the interaction between hydraulic fracture and single natural fracture represented by weakened normal and shear bonds [389]. Eshiet et al. [98] simulated the hydraulic fracturing implemented in materials with mechanical properties resembling rock and soil. Influences of injection parameters and rock properties on hydraulic fracture initiation and propagation are studied using PFC2D [325]. Hofmann et al. [146] simulated simultaneous propagation of multiple hydraulic fractures under different completion design (stage spacing, wellbore spacing, etc.) and treatment parameters. The fracture patterns obtained in these numerical cases are transferred to a finite element reservoir model to investigate the impact of completion design and treatment parameters on the efficiency of fracture networks.

Using a proprietary DEM code similar to PFC, De Pater and Beugelsdijk [84] simulated hydraulic fracture propagation in naturally fractured rocks, where the natural fracture network is represented by breaking bonds along the natural fractures. The simulation results show that the hydraulic fracture does not propagate under low flow rate due to the significant leakoff into natural fractures. Shimizu et al. [293] investigated the influence of heterogeneous particle size and fluid viscosity on initiation and propagation of hydraulic fractures using a DEM code. Analysis of the synthetic acoustic emission from the numerical simulation shows that the acoustic emission produced by tensile failure is normally smaller than that produced by shear failure and shear type acoustic emission with larger energy is normally observed. Wang et al. [321] simulated the initiation and propagation of hydraulic fractures using the coupled Bonded Particle-Lattice Boltzmann Method (BPLBM), an extension of the Discrete Element-Lattice Boltzmann Method (DEM-LBM). The numerical results demonstrate that BPLBM is a promising method in simulating the fluid-solid interactions during hydraulic fracturing at the grain level.

Different from the continuum methods, DEM simulates the hydraulic fracturing from a microscopic perspective [320, 322]. The benefits here are manifold: (1) no extra fracture criterion is needed to govern the fracture propagation; (2) initiation and propagation of hydraulic fracture can be simulated in a unified framework; and (3) there is no need to update the topology with the propagation of hydraulic fracture. However, the relevant parameters need to be calibrated before the application to assure the accurate modelling of the macroscale mechanical behaviour of the rock [249]. A major drawback of DEM is its computational cost. Large particles or blocks (e.g. cm$\sim$dm) are needed to make the simulation of field-scale problems affordable. However, the particles or blocks representing rock grains in microscale or mesoscale problems may lose their physical meaning once their size is overly increased. Another weakness is that the stimulated fracture network is presented by discrete particles, which is not as clear as the mesh surface representation in continuum methods.

• Rigid-Body-Spring Network (RBSN)

Kawai [164] developed the RBSN that has a much better computational efficiency than the FEM. This model was further developed by Bolander et al. [28] to achieve elastic homogeneity by using Voronoi polygon discretization. Recently, the RBSN approach has been adopted for hydraulic fracturing simulation by combining with the TOUGH code developed in Lawrence Berkeley National Laboratory [14, 15, 167]. The flow diagram of TOUGH-RBSN linkages for coupled HM simulation is given in Fig. 19. The fluid pressure, degree of saturation and other hydraulic quantities are solved by TOUHG2 while the displacement (movement of the Voronoi polygons) is computed by RBSN. External modules are used to link the output from one model with the input of another model, as shown in Fig. 19. The spring set between two Voronoi polygons is assumed to break once the corresponding damage index reaches 1 and then new fracture surfaces are generated. In the meantime, an interface node is newly inserted in the model of TOUGH2 once the spring set breaks. The fluid flow inside the fracture is simulated through the fluid exchange between the interface nodes while the leakoff can be simulated via the connectivity between the interface node and the matrix. Using this model, Asahina et al. [15] simulated 3D hydraulic fracture propagation from a borehole with a radius of $1\text{ cm}$ in a $17\text{ cm}$ cubic.

• Variants of Virtual Internal Bond (VIB)

Virtual Multidimensional Internal Bond Model (VMIB) is a variant of Virtual Internal Bond (VIB) model which was developed by Klein and Gao [169] and Gao and Klein [111] for simulating general crack nucleation and growth. In the VIB theory, the macroscopic material is described by material particles and cohesive interactions between them at the microscopic scale, as shown in Fig. 20. The mechanical behaviour of the bonds and macroscopic material properties are related by Cauchy-Born rule of crystal elasticity which equating the strain energy function at the macro-scale to the potential energy at the micro-scale.

Fig. 19

Flow diagram of TOUGH-RBSN linkages for coupled HM simulation [167]

Fig. 20

Schematics of VIB and VMIB models: a computational domain represented by material particles (solid circle) and virtual bonds (solid line) and b material particles bonded with normal bond for VIB and VMIB and shear bond (only for VMIB model)

Zhang and Ge [382] developed the VMIB model by adding a shear effect on the bonds connecting material points in the VIB model, which avoids the fixed Poisson’s ratio in the VIB model. The normal bond stiffness ${{k}_{n}}$ and shear bond stiffness ${{k}_{s}}$ are related to the macroscopic material properties through the following expressions:

$$\begin{aligned} {{k}_{n}}= & {} \frac{3E}{4\pi (1-2\nu )} \end{aligned}$$

(71)

$$\begin{aligned} {{k}_{s}}= & {} \frac{3(1-4\nu )E}{4\pi (1+\nu )(1-2\nu )} \end{aligned}$$

(72)

Zhang and Ghassemi [383] investigated the interaction between hydraulic and natural fractures in 2D by using the VMIB method. Specifically, the propagation and re-initiation of hydraulic fracture are handled by the following strain-based criterion:

$$\begin{aligned} {{\varepsilon }_{1}}\ge \lambda {{\varepsilon }_{t}} \end{aligned}$$

(73)

where ${{\varepsilon }_{1}}$ is the maximum principle strain, ${{\varepsilon }_{t}}$ is the uniaxial tensile strain, and $\lambda$ is a constant coefficient, normally larger than one. The fluid pressure is assumed to be uniform and the nodal force due to the fluid pressure is computed based on the “element” geometry. Crossing, penetration, arrest and offset are represented by setting different loading schemes, fracture shear stiffness and intersection angles.

Huang et al. [151] applied the VMIB model to simulate the propagation of an elliptical fracture driven by hydraulic pressure in a 3D block. Complex geometry of the mixed-mode 3D hydraulic fracture is considered. The fluid pressure is assumed to be uniform along the fracture and constant over time, while the impact is transferred to the mass particles through fracture surface. The failure criterion is embedded into the constitutive relation for bonds. To avoid remeshing, 3D element partition method is adopted.

More recently, Zhang [380] and Zhang and Chen [381] developed Discretized Virtual Internal Bond (DVIB), another variant of VIB, by discretizing the continuous VIB to represent the non-linear elasticity. In the framework of DVIB, the macroscopic material properties are represented by a discrete bond system which is composed of the so-called unit bond cells. The parameters of the microscopic bonds inside the unit cells need to be determined according to macroscopic material properties. Zhang et al. [385] developed a 2D model based on the DVIB method to investigate the effect of pressurization rate, in-situ stresses, orientation of perforation, etc. on hydraulic fracture trajectory. A presumed strain threshold (two times failure strain) is regarded as the fracture propagation criterion. Once the maximum principal strain is over the threshold, new fracture surfaces are assumed to form along the direction perpendicular to the maximum principal strain. Then the uniform fluid pressure is applied on the inner boundary of the fractured unit cell. The model was extended to consider the fluid pressure gradient with Poiseuille’s law in [241].

VMIB and DVIB share a similar formulation with the aforementioned DEM methods and inherit the same advantages. Non-linear elasticity has been considered in the DVIB model.

4.3 Hybrid Continuum/Discontinuum-Based Methods

The applications of continuum-based methods (BEM, FEM, XFEM, FDM, etc.) and the discontinuum-based methods (DEM, RBSN, peridynamics etc.) in hydraulic fracturing simulation have been reviewed in the previous sections. These two groups of methods are both appropriate for specific types of problems according to the associated assumptions. More specifically, the continuum-based methods treat the computation domain as a single continuous body to solve continuum mechanics equations while the discontinuum-based methods treat the material as an assembly of separate blocks or particles for discontinuum-based phenomena [158]. However, in some problems, the transition from continuum to discontinuum may occur due to progressive insertion of discontinuities such as failure, fracture, fragmentation processes, which motivated the development of combined finite-discrete element method (FDEM) [140, 219, 220]. In the framework of FDEM, the concept of DEM is used to model the contact between different solid regions produced by fracturing while FEM is used to analyse deformation of each solid region based on the specific constitutive model. This kind of modelling frameworks are particularly suitable for problems involving progressive fracturing such as failure of jointed rocks, blasting [53, 131, 183, 184, 357]. The popularity of FDEM has been growing steadily over the years, and examples include the Y-Code developed by Munjiza et al. [220], Munjiza [219] and the Elfen developed by Rockfield Software Ltd. [265].

• FDEM with joint elements

Grasselli et al. [126] investigated the influence of bedding planes and natural fracture on the behaviour of hydraulic fracture around wellbore using the 2D FDEM code, Y-Geo developed by Mahabadi et al. [200]. This model includes the following key parts: elastic deformation of finite elements, rigid motion of discrete bodies, contact detection and interaction between discrete elements, and fracturing. Considering only the initial stage of hydraulic fracture propagation is focused here, the uniform fluid pressure is assumed to increase rapidly (100 MPa/s) until the induced fracture extended one diameter from the wellbore and then is kept constant in subsequent numerical steps. Cohesive elements are introduced along the interface between elements to model fracture propagation. Numerical results show that the presence of bedding planes leads to the initiation of multiple hydraulic fractures around the wellbore. Crossing, offset and arrest are also observed. It is worth noting that fracture only propagates along the interfaces between elements. This model was extended to simulate 2D hydraulic fracture propagation in naturally fractured reservoir [195, 388] and 3D propagation of hydraulic fracture from the wellbore [194].

Guo et al. [132] developed a 3D hydraulic fracturing model with an immersed-body approach for coupling fluid and solid. The rock deformation and fracture propagation are simulated with the Solidity program developed by Xiang et al. [344, 345] and Guo et al. [131] based on Y-Code. Different from most of the hydraulic fracturing models where the same mesh and nodes are shared by the solid and fluid simulation, an adaptive fluid mesh over the whole computational domain was adopted for modelling fluid flow inside fracture using Fluidity, an FEM-based fluid code developed in Applied Modelling & Computation Group (AMCG) in Imperial College London [120, 274, 356]. This model was further developed by Obeysekara [228] to investigate the 2D and 3D hydraulic fracture propagation in porous media. Fine shell-mesh is used to discretize the domain inside the natural and hydraulic fractures to capture the fracture permeability (calculated with Poiseuille’s law) accurately while relatively coarse mesh is used for the remaining domain.

Some other programs which have a similar framework as Y-Code have also been used in hydraulic fracturing simulation [159, 160, 355]. Developed by Li et al. [190], Feng et al. [102] and Zhao et al. [386], continuum-based discrete element method (CDEM) is a dynamic explicit framework for simulating progressive failure of geological body. It differs from the common FDEM (e.g. Y-Code) that the maximum tensile criterion and Mohr-Coulomb criterion are used to check the initiation or propagation of fractures (i.e. separation of elements). Using CDEM, Ju et al. [159, 160, 162] studied 2D and 3D propagation of hydraulic fractures in heterogeneous glutenite, where the gravels and natural fractures captured using CT-scan are incorporated into the numerical models and show non-negligible influence on the fracture path.

In the aforementioned models, the joint elements (or cohesive elements) are inserted into the interface between adjoined elements. The discontinuities such as fractures are presented by the breakage of joint elements without change to the mesh topology. No remeshing is conducted along the simulation and a relatively fine mesh needs to be used from the beginning. In essence, this kind of model resembles DEM with the blocks (particles) and bonds replaced by deformable triangular/tetrahedral elements and joint elements.

• Elfen tgr

The commercial software Elfen tgr developed by Rockfield Software Ltd. [265] presents the transition from a continuous medium to a solid with discrete fractures by adaptively inserting cracks into the model with adaptive remeshing. A fracture prediction algorithm is designed to determine whether the hydraulic fracture will propagate or not and to predict the propagation path. The new fracture surface is not restricted in the existing interface between elements. Once a new fracture surface is created, the local mesh around fracture tip is updated followed by a standard mapping for key nodal and element variables. The process is shown in Fig. 21. Both the fluid flow in the fracture and reservoir are simulated with the permeability of fracture determined according to the lubrication theory.

Fig. 21

Fracture propagation and local remeshing: a prediction of new fracture surfaces and b update of local mesh around crack tip

Profit et al. [248] simulated hydraulic fracture propagation in 2D intact or naturally fractured reservoir. The hydraulic fracture model is constituted of three coupled modules dealing with rock deformation, porous flow in reservoir and fluid flow in the fracture respectively. Pore pressure is considered through Biot’s poroelasticity theory and the effective stresses are governed by the combined Mohr-Coulomb or modified Cam-Clay and Rankine cap material model. Poiseuille’s law is considered in simulating the fluid flow inside fracture. Leakoff is governed by the model proposed by Williams [339] based on fluid loss experiments. Natural fractures are modelled with Mohr-Coulomb stick-frictional slip contact regions. Propagation of hydraulic fracture in 2D naturally fractured reservoir with two sets of natural fractures are simulated. The slip failure of natural fractures away from the hydraulic fracture is not observed from the inferred microseismicity, which is different from the numerical results in [223]. The difference may be due to the different parameters used, the model for natural fractures or the scale effect. The capacity of Elfen tgr in modelling hydraulic fracturing in complicated conditions was further demonstrated in [246]. Nonplanar propagation of single hydraulic fracture and interaction between hydraulic fractures are simulated in 3D rock mass. In addition, proppant transport, flowback and clean-up of fracture region and gas and oil production have been added into Elfen tgr, which makes it an integration of hydraulic fracturing simulator and reservoir simulator. Parallel computation techniques have also been applied in the framework to accelerate the simulation. More applications of the program can be found in [160, 161].

4.4 Summary of Diverse Numerical Approaches in Hydraulic Fracturing Simulation

As discussed above, numerous modelling approaches have been applied in hydraulic fracturing simulation, which keeps attracting more research efforts [152, 171, 309, 317, 360, 372] and such new techniques as reduce order modelling [59] and genetic algorithms [181] are gaining attention. Some other potential numerical approaches are discussed in [158]. The simulators based on PFM, DEM and combined FDEM are more promising in terms of simulating complex interactions between hydraulic and natural fractures. The traditional discrete fracture models using FEM and XFEM / GFEM are weaker than smeared fracture approaches such as PFM in terms of simulating complex intersection of fractures in 3D space but they have the advantage to capture sharp fracture surfaces. The combined FDEM seems to be most beneficial for simulating complex hydraulic fracture propagation in naturally fractured reservoirs. The advantages and disadvantages of above numerical approaches in hydraulic fracturing simulation are summarized in Tables  3 and  4.

These hydraulic fracturing models simulate the complex propagation of hydraulic fractures with rigorous governing equations and numerical methods. However, some important aspects have been commonly ignored in these models. First, the slurry with varying concentration and size of proppant is simplified as a Newtonian in most cases or non-Newtonian fluid in some situations, and proppant transport is rarely considered in complex 3D models. Second, some hydraulic fracturing models are limited to lab-scale problems and not capable of simulating real-world geometries of hydraulic fractures. Lastly, the rigorous and complex 3D models are normally computationally expensive, which makes them not popularly used for practical design.

Table 3 Continuum-based methods in hydraulic fracturing simulation

Table 4 Discontinuum-based methods and hybrid continuum/discontinuum-based methods in hydraulic fracturing simulation

5 Commercial Software for Hydraulic Fracturing

Different from some of the numerical models described in Sect. 4, the commercial simulators focus more on practicability and efficiency of the simulation as well as the incorporation of field data. Ideally, besides the fracture propagation simulations reviewed in Sects. 3 and 4, the hydraulic fracturing modelling software should also include the modules for data analysis, automatic generation of pump schedule, post-fracture production analysis, etc. With these modules, a workflow from log analysis to production prediction can be created. In addition, the hydraulic fracturing models in the software generally need to be calibrated with the field measurement of injection pressure and microseismic events. In this section, the widely used and emerging commercial software tools for hydraulic fracturing design are reviewed. The relevant theories and numerical methods underpinning the fracture propagation models in these commercial simulators are discussed and the key features of the software tools are highlighted.

Although over ten software tools are reviewed in this section, the list is not exhaustive given the simulation technologies are constantly developing driven by the growing industrial needs from not only the petroleum industry but also the environmental and geothermal applications. It is worthy to note that the features of these software may change in future versions. The up-to-date information in the following discussions is mainly from the official site of the software and publications by the developers and company. Considering the effectiveness of the software not only depends on their functions but also the capacity of the users, the following discussions provide only a factual summary of relevant information without any preference and recommendations. The software tools are reviewed in the alphabetical order.

5.1 Elfen

Elfen is an advanced FDEM-based software developed by Rockfield Software Ltd. since 1985 for solving a range of geomechanical problems. Apart from the standard software package, another four functional packages specifically for the geomechanical applications in oil & gas industry have also been developed: Elfen fm, Elfen horizon, Elfen wellbore and Elfen tgr.

The focus here is on the Elfen tgr for tight gas reservoir, an “all in one” simulator for hydraulic fracturing. Elfen tgr is applied to hydraulic fracturing using full physics to simulate complex coupled geomechanical and hydraulic systems in 2D and 3D to answer challenging fracture design problems at multiple scales. The details about the computation of rock deformation, fracture propagation, fluid flow are summarized in Sect. 4.3. The features of Elfen tgr are manifold [247]: (1) it is capable of simulating propagation and interaction of 3D nonplanar hydraulic fractures for multi-well, multi-cluster scenarios; (2) models are poro-elasto-plastic, fully coupled with fluid flow in the the propagating fractures as well as within the matrix; (3) stress shadowing effect, hydraulic-natural fracture interactions (DFN stimulation), leakoff, perforation pressure drop, fracture closure, proppant transport, multi-well interference, formation damage, flow back are all accounted for in the analysis to provide realistic representation of the hydraulic fracture network growth; (4) it allows simulating full cycle of stimulation-production-refracturing-production operations; and (5) synthetic microseismicity is computed numerically according to the failure of rock media and is compared against the field microseismicity. These features make Elfen tgr one of the most advanced hydraulic fracture simulators.

A field case of hydraulic fracturing in a heterogeneous reservoir is reported in [264]. The transverse hydraulic fracture initiates from a horizontal wellbore with a true vertical depth of $2900 \text { m}$. The high-resolution profiles of the Young’s modulus, Mode I failure proximity (sum of minimum horizontal stress and tensile strength), vertical stress, pore pressure and Poisson’s ratio versus depth are extracted from the wellbore log data and input into the numerical model. The front of hydraulic fracture after injection of nearly $5 \text { m}^3$ slickwater is shown in Fig. 22.

Fig. 22

Propgation of a hydraulic fracture in a heterogenous reservoir with varying rock properties and stress states versus depth [264]

ELFEN has also been applied in simulating multi-stage hydraulic fractures with stress shadowing effect accurately simulated [266]. Figure 23 shows the stimulated multi-stage hydraulic fractures with 11 clusters spaced $6 \text { m}$ apart. A helical pattern of fractures with a significant asymmetry in all directions emerges due to the stress shadowing effect. These results indicate the shapes of hydraulic fractures may be much more complex than those assumed in classic models reviewed in Sect. 3.

Fig. 23

Fracture propagation and interaction in 3D between multiple horizontal wells in Elfen tgr [266]

5.2 FracCADE

FracCADE, a fracturing design and evaluation software, is a field-validated fracturing simulator developed by Schlumberger Ltd. on proven physical principles of hydraulic fracturing for an optimized treatment [277]. The system incorporates a range of hydraulic fracturing models, from 2D approaches to extensive laterally coupled 3D simulators. It includes a number of complementary modules for optimization of fracturing fluid and proppants, pumping schedules, real-time monitoring, pressure matching, production forecast and economic evaluation. In the module of PropFRAC Placement, KGD, PKN, radial, and cell-based P3D model are included to simulate the fracture geometry. Proppant concentration is solved and screenout due to proppant bridging or dehydration is modelled. The MultiFRAC Placement (MLF) module simulates the simultaneous propagation of multiple hydraulic fractures. The DataFRAC module is used to analyse the field data generated during treatment and to estimate the fracture closure pressure, leakoff coefficient and other related parameters, which helps to improve the design in future. The injection pressure is analysed in the Auto Pressure Match module and the PropFRAC Placement module is executed repeatedly based on a given set of fracture parameters to match the simulated and measured fracturing procedures. The interested reader is referred to [155, 298] for the application of FracCADE in hydraulic fracturing design.

5.3 FracMan

The FracMan software suite is an advanced DFN simulator for the analysis and understanding of heterogeneous and fractured rock masses. It was first released by Golder Associates in 1986 and has been continuously developed and refined within Golder Associates’s FracMan Technology Group founded by William Dershowitz. The software has been applied in many areas including fractured reservoirs, mining/geotechnics, well testing, hydraulic fracturing, radioactive waste management and offers four editions for different purposes: reservoir, geomechanics, nuclear and hydro editions.

One of the most important features distinguishing the FracMan reservoir edition from some other hydraulic fracturing simulators is that natural fractures are explicitly represented in the model as close as they are known according to the well log information, well testing, etc. Instead of using the conventional approach to simulate hydraulic fracture propagation and interaction with complex natural fracture networks (normally complex and time consuming), a hybrid DFN/FEM system is used in FracMan for solving the rock deformation and fluid flow (see Fig. 24). The capacity of efficiently modelling complex fracture networks bypasses many numerical and geometrical challenges encountered in hydraulic fracturing simulation.

The fracture width is computed based on the local effective fluid pressure and rock properties [72, 73, 87]

$$\begin{aligned} w={{p}_{d}}\frac{2(1-v)}{G} \end{aligned}$$

(74)

where $p_{d}$ is the effective fluid pressure in the connected natural fracture network determined by an empirical distribution

$$\begin{aligned} {{p}_{d}}=({{p}_{p}}-\sigma _{0}){{d}_{\max }}\sqrt{1-{{\left( \frac{d}{{{d}_{\max }}} \right) }^{2}}} \end{aligned}$$

(75)

where $p_{p}$ is the pump fluid pressure, $\sigma _{0}$ is the confining stress, $d_{max}$ is the maximum distance considered as part of the hydraulic compartment.

A geomechanical upscaling approach is adopted to consider the change of rock properties due to the effect of natural fractures. The rock stiffness tends to increase due to the fracture inflation. A finite element analysis with a non-conformal mesh is conducted to update the stress field. In this case, the stress shadowing effect, i.e. the interference between fractures, is also considered.

Fig. 24

Simulations of multi-stage hydraulic fractures from multiple horizontal wellbores using DFN-FEM approach in FracMan [73]

Both the induced hydraulic fracture and natural fractures are assumed to propagate along the direction perpendicular to the local minimum principle stress once the tensile failure occurs. The concept of critical stress analysis is used to estimate the behaviour of natural fractures when interacted with the hydraulic fracture. The shear stress applied on the natural fracture is compared with the yielding shear strength computed based on Mohr-coulomb criterion, expressed as

$$\begin{aligned} {{\tau }_{yield}}={{\sigma }_{n}}tan\phi +c \end{aligned}$$

(76)

where ${{\sigma }_{n}}$ is the fracture normal effective stress, $\phi$ the friction angle, and c the cohesion.

For each incremental step of the hydraulic fracture propagation, the volume of fluid in the fracture system needs to be estimated and it should equal the total injected fluid volume. Considering the low permeability of the rock matrix compared with natural fractures, only the leakoff from induced fracture to natural fracture network is considered, while the leakoff from the fracture network to the rock matrix is neglected. A simulation workflow for solving the whole system is given in [73].

To perform hydraulic fracturing design, FracMan has also incorporated other features including proppant transport, synthetic microseismic events, etc. With these features, FracMan has been extensively used to carry out hydraulic fracturing design in the natural gas, deep geothermal and deep mining industries [71, 73, 101, 351].

5.4 FrackOptima

FrackOptima is a hydraulic fracturing design software from FrackOptima Inc. (founded in 2013) [104, 340, 350, 370]. Both the PL3D model and Non Planar 3D hydraulic fracturing models have been incorporated into the simulator. In the Non Planar 3D model, all fractures are assumed to be vertical and can propagate in any horizontal direction.

The rock deformation is solved using DDM based on the linear elastic assumption. The varying stress distribution from layer to layer is considered in the model. The whole elastic fracture matrix relating the fracture width with fluid pressure is constructed through assembling the elastic fracture matrix for each layer based on a continuity equation on all interfaces between layers [350]. For the fluid flow, the coupled equations of the lubrication theory and the continuity relation are solved in a simplified mode by using a modification of successive change of steady states method [340]. Leakoff is controlled by a pressure dependent Carter type leakoff model [340, 350]. As for fracture propagation, a group of virtual elements are placed along the crack front and are allowed to be active as new fracture surface once the potential fluid pressure is large enough to overcome the compressive stress plus rock strength, which can be calibrated from toughness based on the element size. Proppant transport including settling and screenout etc. and the shut-in process have also been simulated. Fracturing fluid and proppant database are included in the software. A comparison of simulated fracture geometry and microseismic signal observed in actual job can be conducted. An example for the propagation of multi-stage hydraulic fractures on horizontal wellbores is shown in Fig. 25.

Fig. 25

Geometry and aperture of multi-stage hydraulic fractures computed in FrackOptima [370]

5.5 FracPro

Maintained and supplied by Carbo Ceramics Inc., FracPro is one of the most widely used hydraulic fracturing design and analysis software in the oil and gas industry [291, 311]. The development of FracPro can be tracked to 1986 [62, 74, 75]. Its key feature is to support real-time analysis of hydraulic fracturing with actual sensor data. With the lumped-parameter 3D model, the problem is greatly simplified to ensure a short execution time. In this model, the crack tip is defined by three variations (upper half-height, lower half-height and fracture length) with the assumption that the upper and lower parts of the fracture are both in an elliptical shape, which plays the role of fracture propagation criterion. The continuity equation is applied on the whole system with fracture volume computed according to key geometrical parameters and shape factor. FracPro does not need to calculate the variations at specific points in the fracture since the effects are integrated into diverse factors which need to be determined according to numerical results from more complex numerical models or field data. In addition, proppant transport modelling has been embedded into the model and is solved using FDM. Leakoff can be handled using different built-in models.

A PL3D model named Frac3D has also been jointly developed by Carbo Ceramics Inc. and Fenix Consulting Delft as an advanced model within the fracture modelling suite of FracPro fracture design and analysis software [148, 244]. Fracture opening is computed using FEM with the rock assumed to be linear elastic, while the 2D fluid flow inside fracture governed by Poiseuille’s law and the continuity equation is solved using FDM [148, 244, 245]. Proppant transport along with the fluid flow is simulated using a two-fluid model. Fracture propagation is controlled by the cohesive zone model. Both the fracture opening and fluid flow are analysed on a structured grid with the local refinement near the crack tip. The Frac3D model has been applied to match microseismic data from the M-Site B-Sand injection [84].

So far, the software has grown into an integrated simulator including hydraulic fracturing design and analysis, economic optimization and reservoir performance. It includes utilities for log analysis, real-time capture, automated met pressure and production history matching, etc. It also allows for multiple fractures, horizontal well fractures and multiple zones with the interference considered as well as different kinds of formations (carbonate, sandstone or even coal). An example is shown in Fig. 26. Built-in libraries for fracturing fluid and proppants are also available. The workflow of unconventional reservoir fracture design using FracPro follows the process of design, analysis and optimization.

Fig. 26

Simulation of interlaced hydraulic fractures in two horizontal wellbores using Fracpro [41]

5.6 GOHFER$^{\text{\textregistered} }$

With over 30 years of development, the Grid Oriented Hydraulic Fracture Extension Replicator (GOFHER$^{\text{\textregistered} }$) software package is a leading multidisciplinary integrated geomechanical fracture simulator and completion optimization tool. It was first created and developed by Barree & Associates LLC and was recently acquired by Halliburton in 2018. The GOHFER$^{\text{\textregistered} }$ software project integrates petrophysics, geology, geophysics, drilling, reservoir and completion, and leads to a coherent and consistent 3D reservoir and geomechanical model for both unconventional and conventional reservoirs.

For fracture modelling, GOHFER$^{\text{\textregistered} }$ allows complex 3D geologic structures in longitudinal and transverse directions to simulate fracture growth in complex folded and faulted regions. The transverse fractures in GOHFER$^{\text{\textregistered} }$ propagate along the plane perpendicular to the direction of horizontal minimum principal stress. Based on the linear-elastic solution of the deformation for an infinite half-space with concentrated load, the normal displacement of fracture face at each grid point over a heterogeneous elastic medium is obtained as:

$$\begin{aligned} u=\int \limits _{\Gamma }{\frac{(1-{{v}^{2}})}{\pi E}p_{n}}d\Gamma \end{aligned}$$

(77)

where $\Gamma$ represents the fracture surface, $p_{n}=p-{{\sigma }_{\min }}-{P}$ the net fluid pressure, p fluid pressure, ${{\sigma }_{\min }}$ the minimum principle stress, and P the existing pore pressure in rock formation.

Fig. 27

Propagation of hydraulic fractures from multiple wellbores in GOHFER$^{\text{\textregistered} }$ [23]

A grid structure is used to solve the elastic rock displacement and allows for vertical and lateral variations of rock properties such as E and $\nu$. Since the rock deformation is directly related to the fluid pressure through Eq. (77), GOHFER$^{\text{\textregistered} }$ is more computationally efficient than other numerical methods such as FEM. Because of its high computational efficiency, GOHFER$^{\text{\textregistered} }$ can model 3D fracture propagation under multi-well and multi-stage scenarios, as shown in Fig. 27. As shown in Fig. 28, the fracture stress-shadow interference between each fracture and stage on each well is modelled by estimating the normal stress surrounding fracture:

$$\begin{aligned} \sigma =\frac{wE}{{12{D}^{{{t}_{e}}}}} \end{aligned}$$

(78)

where D is the distance from the fracture surface and ${{t}_{e}} \in \left( 1,2\right)$ is the inter/intra fracture stress shadow interference factor.

Fig. 28

Illustration of stress shadow propagation for non-orthogonal and asymmetric fractures: blue arrows indicate stress (strain) transmits to offset fracture planes while red arrows indicate stress vectors that do not impact offset fractures [22]

Fracture propagation occurs at the grid nodes where the tensile stress overcomes the pre-set tensile strength and the stress interference from other fractures.

Fluid flow in GOHFER$^{\text{\textregistered} }$ is governed by the coupled equations of Poiseuille’s law, the continuity condition and a pressure-dependent leakoff model, and is solved by using FDM with a regular discretization grid. The fluid rheology can be chosen from the built-in fluid database or defined by the user. The shear-rate and time dependent laboratory test data can also be used to define the fluid rheology. Proppant transport is coupled with fluid flow and solved iteratively for proppant distribution in fractures. Although the pre-existing natural fractures are not modelled explicitly in GOHFER$^{\text{\textregistered} }$, their effect is modelled through pressure dependent leakoff.

GOHFER$^{\text{\textregistered} }$ also includes many pre & post processes such as log analysis and pressure diagnostics. Pressure diagnostics includes DFIT$^\text {TM}$ analysis, step rate analysis for pipe and near-wellbore friction, and ISIP analysis etc. DFIT$^\text {TM}$ analysis provides a powerful toolkit for determining closure pressure, net extension pressure, dominant leakoff magnitude and mechanism, and the reservoir flow capacity. Production model in GOHFER$^{\text{\textregistered} }$ provides time-dependent evolution of pore pressure, stress field and helps to determine evolution of fracture geometry with offset depletion, and it also provides production forecasting and economic optimization. According to the 2017 worldwide survey of the market conducted by Kimberlite International Oilfield Research, 58% of operators choose GOHFER$^{\text{\textregistered} }$ software for their hydraulic fracturing simulation needs and make GOHFER$^{\text{\textregistered} }$ the most popular software in industry for the design, analysis and optimization of hydraulic fracture treatment.

5.7 Kinetix

Developed by Schlumberger Ltd., Kinetix stimulation software suite is an integrated solution for optimizing hydraulic fracturing and acidizing in any reservoir and any well environment [278]. It comprises four components: (1) Kinetix, a reservoir-centric stimulation-to-production software, (2) Kinetix Frac, an integrated fracturing stimulation software, (3) Kinetix Matrix, a matrix stimulation design software, and (4) Kinetix RT, a real-time stimulation optimization software. The first component, Kinextix, is most relevant to this review and is discussed here.

Kinetix reservoir-centric stimulation-to-production software efficiently integrates geology, petrophysics, completion engineering, reservoir engineering, and geomechanics to optimize completion and fracturing designs for a well, a pad, or a whole field [279]. A seamless and comprehensive seismic-to-simulation workflow for multilevel optimization of stimulation designs and production from oil, gas, and condensate reserves is designed. A series of fracture models including PKN, KGD, P3D, PL3D, and UFM (formerly Mangrove) have been incorporated into the software to simulate the hydraulic fracturing in any reservoir, from conventional to unconventional tight sands and shale.

The UFM in Kinetix is a fully coupled numerical model for simulating complex fracture geometries while accounting for reservoir heterogeneity, stress anisotropy, and 3D stress shadowing effects. It efficiently models hydraulic fracture interactions with multilayer natural fractures as it solves for fracture propagation mechanics and proppant transport. The concept of UFM is discussed in detail by [173, 335]. Briefly, UFM can be regarded as a combination of the cell-based P3D model and the enhanced 2D DDM. As shown in Fig. 29, the fractures are all discretised into cells, which is a good compromise between the computational cost, numerical accuracy, and field need. Fracture geometry is computed in the scheme of cell-based P3D model while the stress shadow is considered using 2D DDM with 3D correction [11, 335]. Analytical crossing criterion is incorporated into this model to determine if the hydraulic fracture will cross or penetrate into a natural fracture. Fracture propagation occurs at the crack tips where the stress intensity factor is greater than the rock toughness. A 1D proppant-transport model is adopted along horizontal direction while the settling and bank erosion is computed to track the interface between fluid, slurry, and proppant bank (see Fig. 29) [335].

Fig. 29

Schematic of fracture network and proppant transport in UFM (unconventional fracture model) [19]

When applied in practical design, the DFN as well as the parameters used in the UFM need to be calibrated with the field data such as microseismic data, as shown in Fig. 30. Firstly, a DFN model needs to be generated according to the geological, geophysical and log-based data. Then the fracture geometry can be predicted using UFM with the fracture treatment data and earth model. By adjusting some parameters such as leakoff coefficient, the predicted net pressure need to match with the measurement in field. In addition, the predicted fracture geometry also needs to agree with the pattern of microseismic data. If not, the inputs for UFM including geomechanical model (minimum horizontal stress, rock properties), DFN model and leakoff coefficient need to be adjusted. The workflow is repeated until both the predicted net pressure and fracture geometry match with the field data. The calibration process will likely need a number of wells data to include the variability of geologic properties. Once the model is calibrated, it can improve the completion strategies and treatment design more reliably.

Fig. 30

Workflow for calibration of Unconventional Fracture Model with microseismic data [61]

Once the stimulated fracture network is determined, high-resolution simulation grids (structured or unstructured) are automatically generated for reservoir simulation. The fracture dimensions and conductivities are captured, and the propped and non-propped regions are tracked in the networks.

5.8 MFrac$^\text {TM}$ and MShale$^\text {TM}$

MFrac is a hydraulic fracturing model developed by Meyer & Associates Inc. [204,205,206] and is currently the fracturing design and evaluation simulator in JewelSuite$^\text {TM}$ Reservoir Stimulation application owned by Baker Hughes. It is formulated between the P3D and PL3D models and has grown into a widely used integrated simulator for fracture design and treatment analysis with fully coupled proppant transport and heat transfer. The details of the model are described in [206]. Leakoff is governed by a total leakoff coefficient which can be computed in several different ways. The settling and convection of proppants as well as the heat-up of the fracturing fluid can be considered in the model.

Apart from fracture design, MFrac is also capable of conducting real-time and replay fracture simulation when combined with MView. Production analysis can be conducted through MProd which is fully compatible with MFrac [206]. In this case, an integrated system for treatment optimization is constructed. Propagation of multiple hydraulic fractures from different treatment stages and wellbores have been implemented by considering stress shadowing effect estimated by analytical solutions or sophisticated finite element models.

Fig. 31

Schematic of discrete fracture network in MShale [145]

In MFrac, the effect of natural fractures is ignored and may lead to unreasonable prediction of hydraulic geometry far from the real case. MShale, a DFN simulator is specially designed to model multiple, cluster, complex and discrete fractures in shales or coal (see Fig. 31) [145]. With user-specified fracture network grid, the fracture width and propagation along X-, Y- and Z- directions can be numerically computed. Interaction between multiple fractures can be user-specified or calculated empirically based on the created fractures network. Real-time or replay analysis is also available when combined with MView.

5.9 ResFrac

ResFrac is a fully integrated hydraulic fracturing and reservoir simulator developed by McClure Geomechanics LLC. founded by Mark McClure in 2015. The most important feature of the software is that the full well life cycle from hydraulic fracturing to production is analysed in one seamless simulation. The details of the simulator are comprehensively disclosed in [201, 202]. The fracture width is computed using 3D DDM with the assumption of infinite, linear elastic medium. The hydraulic fracture is discretised into constant displacement rectangular elements. Fracture propagates when the stress intensity factor calculated using the approach in [290] reaches the fracture toughness. The hydraulic fracture propagates along the planar plane perpendicular to the minimum in-situ stress by default or along the direction of locally calculated maximum horizontal stress, which may lead to curving fracture paths.

The fluid flow through the matrix, fracture and wellbore are modelled using FVM with cubic, rectangular and line elements respectively. The fluid flow in matrix is governed by Darcy’s law. A dual porosity model is implemented to account for the fluid loss into natural fractures and secondary fractures. As for the fluid flow in the fracture, general-purpose relations are developed based on their previous work [295] to simulate the process in the stage of hydraulic fracturing and production within the same framework. The relations reduce to the well-known constitutive equations, such as Darcy’s law, Poiseuille’s law, and Forchheimer’s law in limiting cases and smoothly transition between them in intermediate cases. Proppant transport including bulk gravitational convection, gravitational settling, hindered settling, clustered settling, screenout, and the effect of proppant on slurry viscosity is presented. The multiphase flow in the wellbore is simulated using a homogeneous model with the multiphase viscosity calculated according to mass fraction. Fluid exchange between the fracture and matrix is calculated using a 1D subgrid method.

Fig. 32

Propagation of multi-stage hydraulic fractures from two wellbores in ResFrac [263]

As shown in Fig. 32, ResFrac has been applied in the simulation of multi-stage hydraulic fractures and production. Singh et al. [305] presented an example of optimizing multi-stage hydraulic fracturing in unconventional reservoirs using ResFrac, where the in-situ stress and rock properties vary with depth.

5.10 StimPlan$^\text {TM}$

StimPlan$^\text {TM}$ is a complete software package for hydraulic fracture design, analysis and optimization developed by NSI Technologies LLC. A range of fracture geometry simulation options are built within StimPlan, from quick-look P3D models to the PL3D model. With the PL3D model, StimPlan solves the fracture geometry more rigorously using FEM and gives more accurate geometry estimates for multi-layered formations with high property contrast, as demonstrated in [227]. The stress shadowing effect is computed with the modulus multiplier correlations approach or FEM. Fluid flow and proppant transport inside the fracture are solved on a 2D grid and are coupled with the fracture propagation. The fluid rheology can be time- and temperature-dependent. Leakoff can be determined from core testing, previous field experience, or published equations. With these features, StimPlan is capable of simulating the propagation of multi-stage hydraulic fractures from different horizontal wellbores (see Fig. 33).

Fig. 33

Fracture geometry computed from Stimplan-3D

Like many other commercial simulators, StimPlan also has comprehensively integrated toolkit such as fracturing fluid and proppant database, automatic pump schedule, real-time data acquisition, microseismic visualization and modules for reservoir simulation and economic optimization. It has been widely used in the industry [136].

5.11 Xsite

XSite is a full 3D hydraulic fracturing simulator based on the Lattice and Synthetic Rock Mass (SRM) methods by Itasca International Inc. The rock mass is presented by the lattice model consisting of point mass and springs while the existing joints in a fractured rock mass are represented using the smooth-joint model that accurately predicts slip and opening/closing of joints. Spring elastic/strength parameters are calibrated automatically from experimentally tested rock properties including fracture toughness, unconfined compressive, and tensile strengths. The fracture propagation is simulated by the coalesce of micro-cracks (i.e. breakages of springs) which is checked with a criterion based on the fracture toughness.

Fluid flow in the fracture network can be solved with the mechanical simulation in a coupled way or separately. It is modelled as a flow through a network of pipes connecting fluid elements, located at the centres of broken springs or springs intersected with natural fractures. The flow pipe network is updated once new fracture surfaces (i.e. breakage of springs in mechanical model) are generated or a new natural fracture is connected to the hydraulic fracture. An aperture-dependent fracture permeability is used. Leakoff is computed explicitly as the flow into DFN and the porous medium flow into the rock matrix, or as Carter leakoff. Proppant transport and placement logic are included.

With these features, XSite is capable of simulating hydraulic fracturing from multiple stages and clusters in multiple wellbores (see Fig. 34) as well as the propagation of hydraulic fracture in naturally fractured reservoirs with deterministically or stochastically generated discrete fracture networks. Synthetic micro-seismicity can be produced during the simulation. Extensive numerical cases for hydraulic fracturing simulation with Xsite can be found in [107, 387].

Fig. 34

Propagation of multiple hydraulic fractures from a wellbore in XSite [156]

5.12 @Frac$^\text {TM}$

@Frac$^\text {TM}$ is a powerful hydraulic fracturing simulator developed by Advantek International Corporation founded by Ahmed Abou-Sayed in 1999. A PL3D model with a moving mesh system is adopted. Both the rock deformation and fluid flow are solved using FEM, and leakoff is modelled by Carter’s leakoff model. Fracture propagates when the stress intensity factor at fracture tip exceeds the fracture toughness. Proppant transport is also considered. Different from many other simulators, the rock plasticity can also be simulated. The fracture geometry computed using the moving mesh system is shown in Fig. 35 and a schematic for propagation of multiple hydraulic fractures is shown in Fig. 36.

Fig. 35

Fracture geometry computed from a moving mesh system in @Frac

Fig. 36

A schematic for propagation of multiple hydraulic fractures in @Frac

5.13 Summary of Commercial Software for Hydraulic Fracturing Design

Besides the commercial hydraulic fracturing simulators reviewed above, there have been many other software tools developed and used by the petroleum industry during the past decades, such as ENERFRAC by Shell [296, 297], TerraFrac by Terra Tec Inc. [67, 69], TriFac by S.A. Holditch & Associates Inc. [253], HYFRACP3D by Lehigh University [6], and HYFRANC 3D by Cornell fracture group [44]. For various reasons some of these simulation tools have been discontinued.

A total of thirteen commercial software for hydraulic fracturing design from eleven companies are reviewed in this section, and Table 5 summarizes their key features. The P3D and PL3D models are the most widely used fracture geometry models in these commercial simulators. It is because that: (1) the simulators developed in 1970s and 1980s are mostly based on classic models including PKN, KGD, P3D, and PL3D and they have been used in oil and gas industry for much longer time than the full 3D models which emerged much later, and (2) the PL3D model is a good choice to balance between the accuracy of fracture geometry and the computation cost. Real-time simulation is important to guide the hydraulic fracturing treatment in field and cannot be achieved yet by full 3D models due to high computational cost.

Almost all software tools simulate proppant transport and leakoff which are critical for the practical treatment. Propagation of multiple hydraulic fracture is also an essential part with the calculation of stress shadowing effect simplified to varying degrees. The post-fracture production analysis (reservoir simulation) is available in most of the software. The effect of natural fractures can be simulated using the DFN approach with significant simplifications on geometry and/or interaction mechanism in MShale, FracMan, UFM in Kinetix, or using more rigorous numerical methods, for instance, FDEM in Elfen tgr. The injection pressure record and microseismic events are two important field data sets to calibrate the hydraulic fracturing models and have been widely incorporated into the hydraulic fracturing design software. It is common to input the microseismic events into the software to compare with the predicted hydraulic fracture. The microseismic events can also be reproduced according to the rock failure or reactivation of natural fractures, e.g. in Elfen tgr, FracMan, and Xsite.

Table 5 Features of commercial software for hydraulic fracturing design (listed in alphabetical order)

6 Conclusions and Recommendations for Future Work

6.1 Conclusions

Notwithstanding extensive investigations by both academia and industries for over half a century, the topic of hydraulic fracturing simulation is still under rapid development. In order to provide a structured and informative picture of the research field, we try to summarize the rich technical content in a logical framework, while respecting the chronological order of research advancement. Thus, the review is divided into three major parts: the underlying physical processes, the associated numerical modelling methods and the commercial software adopted by the industry. Wherever possible we try to join connections between the physics, method and application.

In Sect. 2, the three fundamental physical processes (rock deformation, fluid flow and fracture propagation) and other secondary processes encountered during hydraulic fracturing treatment are discussed. Solving the coupled three fundamental physical processes is the critical part of most hydraulic fracturing simulators. Proppant transport has a significant influence on the final fracture network and is reviewed separately [19]. It is also highlighted that secondary processes, including leakoff, poroelasticity, effect of natural fractures, bedding planes and anisotropy and heterogeneities of rock media, are often critical to the success of hydraulic fracturing design and evaluation. They need to be properly represented by numerical models.

In Sects. 3 and 4, we review the classic hydraulic fracturing models including the PKN, KGD, P3D and PL3D models as well as the latest approaches using diverse numerical methods. The theories or numerical approaches used for simulating the three basic physical processes are discussed. The classic hydraulic fracturing models developed between the 1950s and the 1980s predict hydraulic fracture with simple geometry, while modern hydraulic fracturing models based on diverse numerical approaches are capable of predicting the complex propagation of hydraulic fracture. The advantages and disadvantages of the various numerical methods are discussed. BEM-based models simulate hydraulic fracturing with relatively low computational cost and have advantages in dealing with 3D non-planar hydraulic fracture. But they are not capable of presenting nonlinear constitutive models and rock heterogeneities. FEM based discrete fracture models are capable of simulating 3D nonplanar hydraulic fracture but have limited ability in dealing with complex topology caused by interactions between hydraulic and natural fractures. Although XFEM/GFEM are developed specifically for fracture problems, they also encounter this problem. Damage-based smeared fracture models have been used for modelling propagation of hydraulic fracture in heterogeneous rock media but the fracture network is fuzzy. PFM has a good capacity in modelling complex interaction between hydraulic fracture and natural fractures and presenting media heterogeneities in 3D space. PFC is suitable for investigating the microscopic mechanisms of hydraulic fracture while 3DEC shows a high capacity in dealing with a complex fracture network. Another powerful numerical approach, FDEM, has also been applied in simulating complex propagation of hydraulic fracture in naturally fractured reservoir, e.g. Y-Geo and Solidity. With a similar framework, CDEM also shows a great capacity of simulating the complex propagation of hydraulic fractures.

Thirteen commercial software packages for hydraulic fracturing design from eleven companies are studied in Sect. 5. Besides the fracture geometry model, the hydraulic fracturing software should also include modules for data analysis, automatic generation of pump schedule, post-fracture production analysis, etc. Proppant transport, temperature-dependent properties of fracturing fluid, varying stress conditions and rock properties in layered formations are more commonly modelled in commercial software than in numerical models in Sect. 4. With calibrations using the field measurement of injection pressure and microseismic events, a workflow from log analysis to production prediction can be created. Currently, most of the widely used design software are still based on P3D and PL3D models, which predict planar hydraulic fractures. The PL3D model is a good choice to balance the accuracy of fracture geometry and the computation cost. Real-time simulation is important to guide the hydraulic fracturing treatment in field and cannot be achieved yet by full 3D models due to high computational cost. The application of full 3D models in field is expected to be promoted by the increasing computing power.

6.2 Recommendations for Future Work

Research in the area of hydraulic fracturing simulation has advanced for several decades, with many significant achievements both in terms of academic understanding and industrial practice. However, the field is still undergoing rapid development, driven by increasing demand from petroleum, environmental and geotechnical industrials. Some of the most demanding or desirable directions for further research are summarized below:

• The interaction mechanism of hydraulic and natural fractures is not completely resolved. Diverse properties of the natural fractures including permeability, cohesion, friction coefficient can all influence the behaviour of the natural fractures when they intersect with the hydraulic fracture. However, current approaches or models for representing and simulating natural fractures in hydraulic fracturing models are largely simplified and often lack consistency.

• There is still a gap between the capacity of hydraulic fracturing simulators and the complexity of practical problems. First, reliable geological information including natural fracture network should be collected and input into the field-scale hydraulic fracturing models. Second, most of the current models either solve the coupled problem accurately with a much simplified fracture geometry or solve the complex fracture geometry with a much simplified model. The capacity of simulating complex 3D hydraulic fracture in reservoir scale needs to be further improved. In the meantime, computational cost remains a bottleneck for high fidelity simulation.

• Modern hydraulic fracturing models based on diverse numerical approaches are able to predict the complex geometry of hydraulic fracture, but are mainly used to investigate specific mechanisms instead of hydraulic fracture treatment design. The input parameters, boundary conditions, numerical scales are not as realistic as the available commercial simulators.

• A realistic perforation strategy supposes to break the rock in a complex manner, which is often significantly simplified in hydraulic fracturing models.