Introduction

The similarity measure is the tool used for many decision-making processes, unclear reasons, data mining, artificial intelligence, measuring instruments, machine learning, and the reasoning of approximation. The primary purpose of similarity measure is that measures the similarity or like portion between two objects. i.e., it utilizes the degree of a similar part and is expressed between 0 and 1(real number) [1,2,3]. Further, similarity measure was defined for interval-valued data, as crisp value is no more effective in decision-making problems. Similarity interval was introduced to evaluate the similarity of interval-valued fuzzy sets, [4,5,6,7]. The similarity was being used as an application to many areas of imprecise nature, including diagnosis of many diseases, ranking purposes, and engineering tools [8,9,10,11,12]. For proceeded more, similarity measure for intuitionistic fuzzy set initialized according to the concept that it demonstrates the membership also non-membership value along with their daily used applications [13,14,15,16]. A Pythagorean fuzzy set determined similarity measure with their valuable existence in various fuzzy environments was in a Pythagorean fuzzy set. The similarity measures of the Pythagorean fuzzy set are also defined in the sense of consideration of similarity among Pythagorean fuzzy sets [17,18,19]. As a fuzzy set and interval-valued fuzzy set are considered as the composing sets of cubic sets, similarity measure was explained in terms of cubic sets [20,21,22]. Similarity measure under cubic Pythagorean fuzzy sets was initialized to illustrate the similarity between two defined sets with the similarity of their composing sets [23]. The effect of priority degrees on the overall result is thoroughly investigated. Furthermore, in the [24] Pythagorean fuzzy set environment, a decision-making strategy is proposed based on these operators [25]. This paper aims to expand on the concepts of PmFSs and offer some additional operations and findings on them. The idea of the Pythagorean m-polar fuzzy relation to selecting the most suitable life partner was used [26]. A bipolar fuzzy soft set (BFSS) is a powerful mathematical tool for dealing with uncertainty and unreliability in real-world situations such as logistics and supply chain management [27]. Some basic properties of the proposed similarity measure are also discussed, such as the SM of any two PFS-sets equals unity if the two PFS-sets coincide [28]. We studied focused on a problem on a linear Diophantine fuzzy graph, where each arc length is assigned a linear Diophantine fuzzy number rather than a real number in this paper. The linear Diophantine fuzzy number can indicate the linear Diophantine fuzzy graph's arc expenses' uncertainty [29]. Single-valued neutrosophic Einstein interactive weighted averaging and geometric operators are proposed using SVNSs, and smooth approximation with interactive Einstein operations [30].

Further, the development made by different researchers in the area of cubic sets and their applications can be seen in [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. The idea of similarity measure was examined as the powerful mechanism used for many years in various fields using these given sets. For similarity evaluation, many other methods included similarity measures of Euclidean, Manhattan, Chebyshev, Minkowski, cosine, Pearson, Mahalanobis, SED Jaccard, Levenshtein, Dice, Jensen Shannon, Canberra, Hamming, Spearman, Chi-square, and so on. These tools are used in many areas of fuzzy environments to analyze similarities among different sets. In science, similarity measure expresses how the samples of data are closely related, and the concept of dissimilarity is how the data models are diverse or disparate. The similarity measure of the overlapping ratio indicated a set's similarity and dissimilarity to find a given set's overall similarity. The fact is that we discussed in a fuzzy environment that similarity measure has already been under observation. These similarities only find similarities between the sets of positive impacts. It needs to express the negative similarity of sets.

We define the overlapping ratio of the N-Pythagorean fuzzy set and N-interval-valued Pythagorean fuzzy set to initialize the negative similarity. Then we define the overlapping ratio for N-cubic Pythagorean fuzzy sets. Also, we describe the similarity of N-Pythagorean fuzzy sets and N-interval-valued Pythagorean fuzzy sets. After that, we initialize the similarity measure of the N-cubic Pythagorean fuzzy set. Also, demonstrate the comparison of two popular plagiarism checker software using similarity measure of overlapping ratio under the N-cubic Pythagorean fuzzy sets. In this study, we show that our method produces intuitively appealing results even when the similarity is analyzed using a graph visualization method. In our technique (the new measure), we compare two N-cubic Pythagorean fuzzy sets, i.e., with a measure that uses two functions to represent N-cubic Pythagorean fuzzy sets for comparison. While evaluating the results of our new measure's comparison, we draw a graph of the new similarity measure between two N-cubic Pythagorean fuzzy sets, where the membership value of N-interval valued Pythagorean fuzzy sets compares to the membership function of second N-cubic Pythagorean fuzzy sets, and non-membership value corresponds to non-membership value of this set.

Background

We will start through the review of similarity measures. First, we revise the definition of similarity measure in such a way:

Definition [24]

A set \(A=\left\{\left(x,\mu \left(x\right),\vartheta (x)\right)|x\epsilon X\right\}\) is called the Pythagorean fuzzy set, where \(\mu :X\to [\mathrm{0,1}]\) and \(\vartheta :X\to [\mathrm{0,1}]\) and \({0\le \mu }^{2}\left(x\right)+{\vartheta }^{2}\left(x\right)\le 1.\)

Definition [46]

A set \(A=\left\{\left(x,\mu \left(x\right),\vartheta (x)\right)|x\epsilon X\right\}\) is called N-Pythagorean fuzzy set, where \(\mu :X\to [-\mathrm{1,0}]\) and \(\vartheta :X\to [-\mathrm{1,0}]\) and \({-1\le {(-1)}^{2\left(2\right)+1}(\mu }^{2(2)}\left(x\right)+{\vartheta }^{2(2)}\left(x\right))\le 0.\)

Example

Let X = {x}. Then A = {x, \(\mu \left(x\right)\) = − 0.7, \(\vartheta (x)\) = − 0.5} is a N Pythagorean fuzzy set.

Definition [46]

A set \(A=\left\{\left(x,\widetilde{\mu }\left(x\right),\widetilde{\vartheta }(x)\right)|x\epsilon X\right\}\) is called interval valued N-Pythagorean fuzzy set, where \(\widetilde{\mu }:X\to D[-\mathrm{1,0}]\) and \(\widetilde{\vartheta }:X\to D[-\mathrm{1,0}]\) and \({-\widetilde{1}\le {(-1)}^{2\left(2\right)+1}(\widetilde{\mu }}^{2(2)}\left(x\right)+{\widetilde{\vartheta }}^{2(2)}\left(x\right))\le \widetilde{0}.\)

Example

Let X = {x}. Then Ã = {< x, [− 0.6, − 0.5], [− 0.4, − 0.3] >} is an interval-valued N Pythagorean fuzzy set.

Definition [46]

A set \(A=\left\{\left(x,\widetilde{\mu }\left(x\right),\vartheta (x)\right)|x\epsilon X\right\}\) is called N-cubic Pythagorean fuzzy set, where \(\widetilde{\mu }\) is an N-interval valued Pythagorean fuzzy set and \(\vartheta\) is N-Pythagorean fuzzy set.

Example

Let X = {x}. Then NA = {x, < [− 0.8, − 0.7], [− 0.5, − 0.2], (− 0.8, − 0.2) >}, is an N-cubic Pythagorean fuzzy set.

Definition [1]

A similarity measure is a real-valued mapping \({S}^{^{\prime}}\)(E, F) → [0, 1] that describes the similar area between objects (E,F). Basically, the area that is similar between objects lies between the interval [0, 1] such that 0 specify that objects are totally disjoint and 1 specify that objects behave alike. The basic properties of similarity measure are as under below for the sets E, F and G.

Boundedness: 0 ≤ \({S}^{^{\prime}}\)(E, F) ≤ 1.

Symmetry: \({S}^{^{\prime}}\) (E, F) = \({S}^{^{\prime}}\)(F,E).

Reflexivity: \({S}^{^{\prime}}\)(E, F) = 1 ⇐⇒E = F.

Transitivity: If E ⊆ F ⊆ G then \({S}^{^{\prime}}\)(E, F) ≥ \({S}^{^{\prime}}\)(E, G).

Definition [5]

The overlapping ratio (OV) of an interval A within a pair of intervals {A, B} utilizes the cardinality of the alike of the given intervals pair divided by the size of an interval as:

$$\mathrm{OV }(\mathrm{A},\mathrm{ B})\hspace{0.17em}=\frac{\mid A \cap B\mid }{\mid A\mid },$$

such that, |A ∩ B | be the cardinality of the common portion of intervals pair and |A| be the cardinality of A.

Remarks

In an interval A having a cardinality = 0, i.e., |A|= 0, OV (A, B) = 0. The overlapping ratio for the intervals pair will satisfy one of the cases given below:

1) OV (A, B)=1 if A is like B,

2) OV (A, B) =0 if A is different from B,

3) 0 <OV (A, B)< 1, else.

Definition[5]

The similarity measure using overlapping ratio SOR for the intervals pair,

A and B, is the t-norm of inverse overlapping ratios, defined as below:

SOV (A, B) = T (OV (A, B), OV (B, A)) such that T is the t-norm.

Similarity measures of n-cubic pythagorean fuzzy set

The purpose of initiating this concept of similarity measure is the evaluation of the similarities of two N-cubic Pythagorean fuzzy set. To evaluate overall similarity, we consider reciprocal similarity along with similarity measure.

Overlapping ratio for N-Pythagorean fuzzy set

Definition:

The overlapping ratio of the item set A having a set {A, B} is the cardinality of the union of the pair divided by the cardinality of given N-Pythagorean fuzzy set i.e., A. the.

$$\mathrm{OV }(\mathrm{A},\mathrm{ B}) = \frac{\mid A \cup B\mid }{\mid A\mid }$$
(a)

where \(\mid A \cup B\mid\) be the cardinality of the union of A and B. also, \(\mid A\mid\) be the cardinality of set A.

Remark

For any N-Pythagorean fuzzy set with the cardinality of zero i.e., \(\mid A\mid\)= 0, OV (A, B) is the set to 0. Then, the overlapping ratio for N-Pythagorean fuzzy set defined by Eq. (a) satisfies the given one of the following cases:

  1. a)

    OV (A, B) = − 1, when both A and B sets are similar.

  2. b)

    OV (A, B) = 0, when both A and B sets are different.

  3. c)

    − 1 \(<\mathrm{OV}(A, B)<\) 0, otherwise.

Equation (a) implies that OV (A, B) = \(\frac{\mid {\cup }_{j\epsilon A,B}{\mu }_{j}\mid }{\mid {\mu }_{A}\mid }\) and \(\frac{\mid {\cup }_{j\epsilon A,B}{\eta }_{j}\mid }{\mid {\eta }_{A}\mid }\), where \(\mid {\cup }_{j\epsilon A,B}{\mu }_{j}\mid\) is the cardinality of the union of members of the pair {A, B}, \(\mid {\mu }_{A}\mid\) be the cardinality of membership of set A and \(\mid {\cup }_{j\epsilon A,B}{\eta }_{j}\mid\) is the cardinality of the union of non-membership of the pair {A, B},\(\mid {\eta }_{A}\mid\) be the cardinality of the non-membership of A.

Example: Let A = {< x/ − 0.6, − 0.7 >} and B =  < y / − 0.8, − 0.5 > be two NPFS then

$$\mathrm{OV }(\mathrm{A},\mathrm{ B}) =\frac{\mid {\cup }_{j\epsilon A,B}{\mu }_{j}\mid }{\mid {\mu }_{A}\mid }\mathrm{ and}\frac{\mid {\cup }_{j\epsilon A,B}{\eta }_{j}\mid }{\mid {\eta }_{A}\mid }$$

OV (A, B) = <− 1, − 0.71>

Overlapping ratio for N-interval valued Pythagorean fuzzy set

Definition:

The overlapping ratio of the item set C having a sets {C, D} is the cardinality of the union of the pair divided by the cardinality of given N-interval valued Pythagorean fuzzy set i.e., C. the

$$OV(C, D) =\frac{\mid C \cup D\mid }{\mid C\mid }$$
(b)

where \(\mid C\cup D\mid\) be the cardinality of the union between C and D. also, \(\mid C\mid\) be the cardinality of set C. Eq (b) implies that OV (C, D) = \(\frac{\mid {\cup }_{j\epsilon C,D}{\mu }_{j}\mid }{\mid {\mu }_{C}\mid }\) and \(\frac{\mid {\cup }_{j\epsilon C,D}{\eta }_{j}\mid }{\mid {\eta }_{C}\mid }\), where \(\mid {\cup }_{j\epsilon C,D}{\mu }_{j}\mid\) be the cardinality of the union of members of the pair {C, D}, \(\mid {\mu }_{C}\mid\) be the cardinality of membership of set C and \(\mid {\cup }_{j\epsilon C,D}{\eta }_{j}\mid\) be the cardinality of the union of non-membership of the pair {C, D},\(\mid {\eta }_{C}\mid\) be the cardinality of the non-membership of C, where μ, η are the N-intervals (Fig. 1).

Fig. 1
figure 1

Similarity of two N-Pythagorean fuzzy sets

Full size image

Example: Let C = {< x/ [− 0.8, − 0.6], [− 0.6, − 0.5] >} and D =  < y / [− 0.7, − 0.5], [− 0.5,  − 0.3] >} be two NIVPFS then.

$$\mathrm{OV }(\mathrm{C},\mathrm{ D}) = \frac{\mid {\cup }_{j\epsilon C,D}{\mu }_{j}\mid }{\mid {\mu }_{C}\mid }\mathrm{ and }\frac{\mid {\cup }_{j\epsilon C,D}{\eta }_{j}\mid }{\mid {\eta }_{C}\mid }$$

OV (A, B) = <− 1, − 1>

Overlapping ratio for N-cubic Pythagorean fuzzy set

Definition:

The overlapping ratio of item set X having a sets {X, Y} is the cardinality of the union of the pair divided by the cardinality of the given N-cubic Pythagorean fuzzy set i.e., X. the

$$\mathrm{OV }(X, Y) = \frac{\mid X \cup Y\mid }{\mid X\mid }$$
(c)

where \(\mid X\cup Y\mid\) be the cardinality of the union between X and Y. also, \(\mid X\mid\) be the cardinality of set X. Eq (c) implies that OV (X, Y) = \(\frac{\mid {\cup }_{j\epsilon X,Y}{\mu }_{j}\mid }{\mid {\mu }_{X}\mid }\) and \(\frac{\mid {\cup }_{j\epsilon X,Y}{\eta }_{j}\mid }{\mid {\eta }_{X}\mid }\), where \(\mid {\cup }_{j\epsilon X,Y}{\mu }_{j}\mid\) be the cardinality of the union of members of the pair {X, Y}, \(\mid {\mu }_{X}\mid\) be the cardinality of membership of set X and \(\mid {\cup }_{j\epsilon X,Y}{\eta }_{j}\mid\) be the cardinality of the union of non-membership of the pair {X, Y},\(\mid {\eta }_{X}\mid\) be the cardinality of the non-membership of X.

Or in simple words, OV (X, Y) =  < OV (A, B), OV (C, D) > .

Example: let X = {< x/ [− 0.9, − 0.7], [− 0.6, − 0.4], (− 0.5, − 0.8) >} and Y = < y / [− 0.8, − 0.6], [− 0.7, − 0.5], (− 0.4, − 0.7) >} be two NCPFS then.

$$\mathrm{OV }(\mathrm{X},\mathrm{ Y}) = \frac{\mid {\cup }_{j\epsilon X,Y}{\mu }_{j}\mid }{\mid {\mu }_{X}\mid }\mathrm{ and}\frac{\mid {\cup }_{j\epsilon X,Y}{\eta }_{j}\mid }{\mid {\eta }_{X}\mid }$$

OV (X, Y) = <− 1, − 1>

Similarity measure of N-Pythagorean fuzzy set

Definition:

The similarity measure using overlapping ratio \({S}_{OV}\) for the pair of N-Pythagorean fuzzy set is the t-norm of their inverse overlapping ratios, as

$${S}_{OV}(\mathrm{A},\mathrm{ B})\hspace{0.17em}=\hspace{0.17em}{T}_{N}(\mathrm{OV }(\mathrm{A},\mathrm{ B}),\mathrm{ OV }(\mathrm{B},\mathrm{ A}))$$
(d)

where \({T}_{N}\) be the t-norm of NCPFN’s.

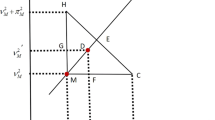
This graph demonstrates that grey portion is similar that defines the similarity measure clearly:

Similarity measure of N-interval valued Pythagorean fuzzy set

Definition:

The similarity measure using overlapping ratio \({S}_{OV}\) for the pair of N- interval-valued Pythagorean fuzzy set (C, D) be the t-norm of their inverse overlapping ratios defined as;

$${S}_{OV}^{^{\prime}}(\mathrm{C},\mathrm{ D})\hspace{0.17em}=\hspace{0.17em}{T}_{N}^{^{\prime}}(\mathrm{OV }(\mathrm{C},\mathrm{ D}),\mathrm{ OV }(\mathrm{D},\mathrm{ C}))$$
(e)

where \({T}_{N}^{^{\prime}}\) is a t-norm of NCPFN’s.

The Fig. 2 clearly explains the like portion of two N-interval valued Pythagorean fuzzy sets illustrated as:

Fig. 2
figure 2

Similar portion of two interval-valued Pythagorean fuzzy sets

Full size image

Similarity measure for N-Cubic Pythagorean fuzzy set

Definition:

The similarity measure using overlapping ratio \({S}_{OV}^{*}\) for the pair of N-cubic Pythagorean fuzzy set (X, Y) is the t-norm of their inverse overlapping ratios defined as:

$$S_{{OV}}^{*} (X,Y) = T_{N}^{*} \{ T_{N} (OV(A,B),OV(B,A)),T_{N}^{\prime} (OV(C,D),OV(D,C))\}$$
(f)

where \({T}_{N}^{*}\)(t-norm of N-cubic Pythagorean fuzzy sets) is a t-norm of NCPFN’s.

Figure. 3 determines the similar portion of two N-cubic Pythagorean fuzzy sets in a better way.

Fig. 3
figure 3

Similar portion of N-cubic Pythagorean fuzzy sets

Full size image

Example: Let X = {< x/ [− 0.9, − 0.7], [− 0.6, − 0.4], (− 0.5, − 0.8) >} and Y =  < y / [− 0.8, − 0.6], [− 0.7, − 0.5], (− 0.4, − 0.7) >} be two NCPFS then.

OV (X, Y) = < − 1, − 1>

Also,

OV (Y, X) = < − 1, − 1>

$${T}_{N}^{*}(\mathrm{OV }(\mathrm{A},\mathrm{ B}),\mathrm{ OV }(\mathrm{B},\mathrm{ A}))\hspace{0.17em}=\hspace{0.17em}{T}_{N}^{*}(<\hspace{0.17em}- 1, - 1\hspace{0.17em}>\hspace{0.17em}, \hspace{0.17em}<\hspace{0.17em}- 1, - 1\hspace{0.17em}>))$$

Then,\({T}_{N}^{*}\) satisfied following conditions:

  • Boundedness.

  • Commutativity.

  • Reflexivity.

So \({T}_{N}^{*}\) is the t norm.

Properties of the similarity measure using overlapping ratio

Following are some characteristics of the similarity measure using overlapping ratio.

(Boundedness)

\({S}_{OV}^{*}\) is bounded by [− 1, 0].

The boundary property of the t-norm \({T}_{N}^{*}\) are (a, − 1) = (− 1, a) = a and (a, 0) = (0, a) = 0, ∀a ∈ [− 1, 0]. When a is the overlapping ratio of NCPFN’s, it always lies within an interval [− 1, 0]. Which implies,\({S}_{OV}^{*}\) is also bounded by [− 1, 0].

(Symmetry)\({S}_{OV}^{*}(X, Y)\)follows the property of symmetry. That is,

$${S}_{OV}^{*}(X, Y)={S}_{OV}^{*}(Y, X)$$

The t-norm \({T}_{N}^{*}\) is symmetric. Therefore,\({S}_{OV}^{*}\)(X, Y)is also symmetric.

(Reflexivity)

\({S}_{OV}^{*}\)(X, Y)satisfied the reflexivity. That is, \({S}_{OV}^{*}\)(X, Y) = − 1 ⇐⇒X = Y.

If X = Y, then OV(X, Y) = OV(Y, X) = − 1. As the boundary conditions i.e.,\({T}_{N}^{*}\), (− 1, − 1) = − 1, so,\({S}_{OV}^{*}\)(X, Y) = − 1. Alternatively, \({S}_{OV}^{*}\)(X, Y) = − 1 means that both OV (X, Y) and OV (X, Y) = − 1. Which exist only when X and Y are same intervals. Where X, Y and Z are the NCPFN’s.

Application

In previous knowledge, college students at California State University, Northridge, delivered some information about plagiarism using software for plagiarism detection. Advance, look at, 1/2 of the scholars in two training have been randomly decided on and using the teachers that their time papers might use for plagiarism the software. Students have no more extended information about the software program that might be used. The workers thought that scholars that have been warned about the usage of the software could plagiarize less than learners were not now. However, the caution had not affected. In a recent study, college students wrote to which that chain of two papers was initialized. Their know-how in detecting plagiarism programs changed oppositely related to the rates of plagiarism on the advanced paper. However, the recent article determined no relation between information and plagiarism. Instead, individuals have attempted to attract repeatedly from the same assets of plagiarized fabric throughout documents.

Several softwares used for plagiarism detection are listed below:

Grammarly, Prowriting Aid, Copyscape, Writer.com, Turnitin, paper Rater, Unicheck, PlagScan, DMCA Scan, Plagiarism checker, iThenticate, etc.

Comparison between two plagiarism software (X and Y)

Software(X) was made for classroom use and is planned for assessing students' work. The University people group has free admittance to two diverse electronic creativity checking tools outfitted to assist authors with keeping away from plagiarism. The following is a short outline of individuals and how interesting to handle them. Software(X) and Software(Y) expect entries to be created by the initial developer. They have no idea for used by other people.

Software(X)

Software(X) has been developed explicitly for classroom use and planned for checking on students' jobs. Like the administration, it can be coordinated into Canvas courses and permits the trainer to view reports of students' ask. It looks at students' tasks of about 60 billion pages, about 600 million student papers that have already been added to the database of this software: and more than 100 million articles from professionals. Submitted articles are added to a database of material from institutions worldwide.

Software(Y)

The software is supposed to accommodate educational writers in warding off plagiarism and copyright neglect while making ready gadgets for e-books and is NOT supposed for lecture room use. This software is considered for editors to examine articles submitted before the booklet. Papers judgment using this software are NOT introduced to or recorded on another database.

In this section, the similarity measure of N-cubic Pythagorean fuzzy sets for the overlapping ratio is used to compare two popular software, i.e., Software(X) and Software(Y).

Let us suppose a set of software A = {X(A1), Y(A2)} along with their parameters, and the set of parameters are:

B = {b1(through publications), b2(online internet sources), b3(group members)}.

Assume that a software, with respect to all features or sources, can be illustrated as by N-cubic Pythagorean fuzzy set:

C = {(b1, [− 0.8, − 0.6], [− 0.6, − 0.4]), (b2, [− 0.7, − 0.5], [− 0.8, − 0.5]), (b3, [− 0.9, − 0.7], [− 0.5, − 0.3])}.

Also, for each software can be observed by NCPFN, s along with the parameters given as below:

A1(X) = {(b1, [− 0.8, − 0.7], [− 0.6, − 0.5]), (b2, [− 0.9, − 0.7], [− 0.6, − 0.4]), (b3, [− 0.9, − 0.8], [− 0.7, − 0.5])}.

A2(Y) = {(b1, [− 0.6, − 0.4], [− 0.7, − 0.3]), (b2, [− 0.8, − 0.7], [− 0.6,− 0.5]), (b3, [− 0.7, − 0.5], [− 0.6, − 0.3])}.

Now, our aim is to classify the software C in one of the sets of software’s \({A}_{j}\) (j = 1,2). For this purpose, the proposed method has been evaluated given in Table 1 from C to \({A}_{j}\)(j = 1, 2).

Table 1 Comparison of two software’s using proposed approach
Full size table

According to the law the maximum value of the similarity measure between two NCPFN, s.

After the numerical discussion given in Table 1, we conclude the following results.

  • We analyzed that the features of software C are 10 \(\%\) like A1(X software) in a negative sense as well as the sources of software C is 30 \(\%\) like A2(Y software) in negative nature.

  • In negative sense, we may achieve that the similarity measure of A2(Y software) is much than A1(X software).

  • By using the idea of maximum degree, the degree of A1 is much greater than A2 which means that C software relate to X software. so, A2 is preferable than A1.

Comparison analysis

In a comparative analysis, we establish three different sets (A1, A2, C) and use predefined measures of similarity, dice, and jaccard for comparison to identify the similarity between A1 and C, as well as A2 and C, which declare the novelty of our proposed approach of similarity measure of overlapping ratio.

The following Table 2 shows the similarities:

Table 2 Comparison Analysis between the existing and our proposed method
Full size table

In this research, we present a new similarity measure that computes the overall similarity of a pair of N-cubic Pythagorean fuzzy sets by considering their common similarity. We employed the over-lapping ratio of the specified sets inside the pair to capture the asymmetric likeness. We've also shown that the new measure meets all of the fundamental characteristics of a similarity measure.

Finally, we used synthetic datasets to compare the behavior of the proposed measure to the well-defined measures of similarity, Jaccard, and Dice similarity measures. The findings reveal that the proposed similarity measure is more sensitive to changes in set width and invariant and linear.

Conclusion

In this article, we defined a new concept of similarity measure of N-cubic Pythagorean fuzzy set based on overlapping ratio by overlapping two N-cubic Pythagorean fuzzy sets after representing the overlapping ratio N-interval valued Pythagorean fuzzy sets and N-Pythagorean fuzzy sets. We describe the similarity measure of N-cubic Pythagorean fuzzy set, N-interval valued Pythagorean fuzzy set, and N- Pythagorean fuzzy sets. Further, we apply this similarity measure for finding the comparison between two software related to plagiarism detectors, i.e., Software(X) and Software(Y). Finally, we reveal the efficacy of the new suggested similarity measure. This similarity measure will be used in many decision-making processes to analyze similarities negatively.

Future studies could include applications of the suggested overlapping ratio similarity metric in multi-criteria decision making (MCDM) and research analysis. A similarity measure for probabilistic N-cubic Pythagorean fuzzy sets were developed to characterize stochastic and non-stochastic uncertainty in a single framework. Future studies could focus on creating an independent module that uses an overlapping ratio similarity metric for existing expert or intelligent systems, software benefits, and online browsers.